Java Binary Tree Logical Errors
I include here the code for a binary tree. There are several problems with the code. The tree is empty at first, then values are inserted. The first value will be at the top. The next value will be on the first values left side if it is smaller then the first value. It will be placed on the right side if it is larger then the initial value. This value will be the first values child node, and the first value will be its parent. When a value has both a left and a right child node, those nodes again will create new child nodes by the same logic when new values are inserted in the tree. In this example I will use the values 1 3 4 10 12 13 14 15 16 20 21 28 29 30 39. I will then delete value 10, and see if I can re-arrange the tree correctly. The initial tree is supposed to look like as in figure A.
1) When I delete the node with value 10 I follow the logic displayed in figure B. Everything seems to work OK, and all the numbers that remain are displayed, but when searching for all the values, the mechanism seems to report that some of the numbers are missing. Just after listing them in order. Example:
"The tree in a sorted display: 1 3 4 14 12 13 15 16 20 21 28 29 30 39
Is 3 in the tree: true
Is 4 in the tree: true
Is 1 in the tree: true
Is 10 in the tree: false
Is 12 in the tree: false
Is 13 in the tree: false
Is 14 in the tree: true
Is 16 in the tree: true
Is 20 in the tree: true
Is 21 in the tree: true
Is 28 in the tree: true
Is 29 in the tree: true
Is 30 in the tree: true
Is 39 in the tree: true"
This happens only when deleting 10(left side child node), but not 28(right side child node).
2) The order of the numbers seems to get juggled around after deletion. I have not been able to figure out why. After deleting node with value 10, I get this order: 1 3 4 14 12 13 15 16 20 21 28 29 30 39
Here you can see that 14 is placed wrong. This does not happen when deleting node with value 28.
Figure A:
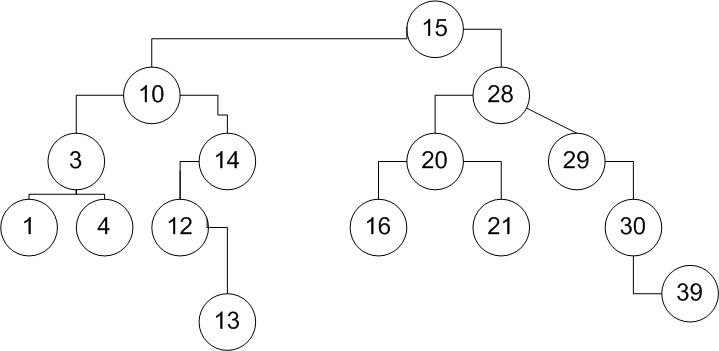
Figure B:
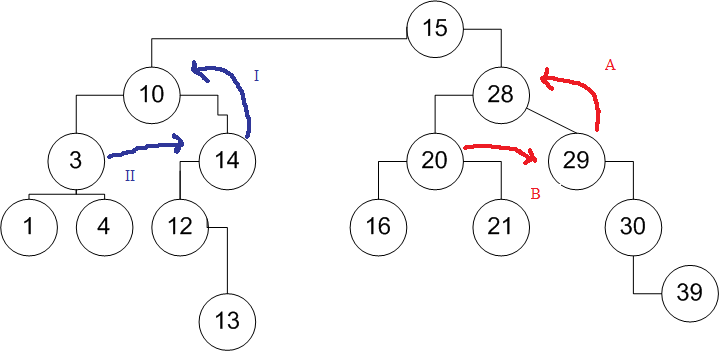
When deleting right side nodes:
We start by simulating deletion of 28.
A) 29 takes 28's place.
B) We ask node at 29 to find a new space for 20.
Then we simulate deletion of 10.
I) 14 takes 10's place.
II) We ask 14 to find new space for 3.
The logic is the same in both examples, only handling different sides of a given node(depending on what side the node is on that is being deleted).
1) When I delete the node with value 10 I follow the logic displayed in figure B. Everything seems to work OK, and all the numbers that remain are displayed, but when searching for all the values, the mechanism seems to report that some of the numbers are missing. Just after listing them in order. Example:
"The tree in a sorted display: 1 3 4 14 12 13 15 16 20 21 28 29 30 39
Is 3 in the tree: true
Is 4 in the tree: true
Is 1 in the tree: true
Is 10 in the tree: false
Is 12 in the tree: false
Is 13 in the tree: false
Is 14 in the tree: true
Is 16 in the tree: true
Is 20 in the tree: true
Is 21 in the tree: true
Is 28 in the tree: true
Is 29 in the tree: true
Is 30 in the tree: true
Is 39 in the tree: true"
This happens only when deleting 10(left side child node), but not 28(right side child node).
2) The order of the numbers seems to get juggled around after deletion. I have not been able to figure out why. After deleting node with value 10, I get this order: 1 3 4 14 12 13 15 16 20 21 28 29 30 39
Here you can see that 14 is placed wrong. This does not happen when deleting node with value 28.
Figure A:

Figure B:

When deleting right side nodes:
We start by simulating deletion of 28.
A) 29 takes 28's place.
B) We ask node at 29 to find a new space for 20.
Then we simulate deletion of 10.
I) 14 takes 10's place.
II) We ask 14 to find new space for 3.
The logic is the same in both examples, only handling different sides of a given node(depending on what side the node is on that is being deleted).
class SubTree {
private SubTree rightTree = null;
private SubTree leftTree = null;
private SubTree parent = null;
private int value = 0;
public SubTree(int value) {
this.value = value;
}
public SubTree(int value, SubTree parent) {
this.value = value;
this.parent = parent;
}
public void insertValue(int newValue) {
if (value >= newValue) {
if (leftTree != null) {
leftTree.insertValue(newValue);
} else {
leftTree = new SubTree(newValue, this);
}
} else {
if (rightTree != null) {
rightTree.insertValue(newValue);
} else {
rightTree = new SubTree(newValue, this);
}
}
}
public String toString () {
String returString = "";
if (leftTree != null) {
returString = leftTree.toString() + " ";
}
returString = returString + value;
if (rightTree != null) {
returString = returString + " " + rightTree.toString();
}
showObject();
return returString;
}
public boolean lookForValue(int søkeVerdi) {
if (søkeVerdi == value) {
return true;
}
if (value > søkeVerdi) {
if (leftTree != null) {
return leftTree.lookForValue(søkeVerdi);
} else {
return false;
}
} else {
if (rightTree != null) {
return rightTree.lookForValue(søkeVerdi);
} else {
return false;
}
}
}
public boolean deleteValue(int value) {
if (this.value == value) {
//If we have found node with right value, we have to find if it has any child nodes
if ((rightTree == null) && (leftTree == null)) {
/**This node has no child, it can be linked off the tree.*/
if(value <= this.parent.getValue()) { //We are on left side, and we will relink there at the parent
this.parent.relink(0, null);
} else { //We are on the right side, and we relink there at the parent
this.parent.relink(1, null);
}
//At the end we relink this objects backreference to parent:
this.parent = null;
return true;
} else if (((rightTree == null) && (leftTree != null)) || ((rightTree != null) && (leftTree == null))) {
/**The node has only one child node. We link over this node to the child */
if(value <= this.parent.getValue()) { //We are on left side, and we link there over this object to this objects rightTree
if ((rightTree != null) && (leftTree == null)) this.parent.relink(0, this.rightTree);
if ((rightTree == null) && (leftTree != null)) this.parent.relink(0, this.leftTree);
this.rightTree = null;
} else { //Or else we are on the right side, and we link there over this object to this objects leftTree
if ((rightTree != null) && (leftTree == null)) this.parent.relink(1, this.rightTree);
if ((rightTree == null) && (leftTree != null)) this.parent.relink(1, this.leftTree);
this.leftTree = null;
}
//At the end we relink this objects reference to the parent:
this.parent = null;
return true;
} else {
/**The noden has two child nodes, these have to moved correctly and placed correctly under the parent node */
if(value <= this.parent.getValue()) { //We are on the left side, we link right child node on left side at the parent
//We then ask the right child node to find new space for the left childnode
this.parent.relink(0, this.rightTree);
this.rightTree.giveNewPlace(this.leftTree);
this.rightTree = null;
this.leftTree = null;
this.parent = null;
} else { //Or else we are on the right side, and we link right child node on the right side at the parent
this.parent.relink(1, this.rightTree);
this.rightTree.giveNewPlace(this.leftTree);
this.rightTree = null;
this.leftTree = null;
this.parent = null;
}
this.parent = null;
return true;
}
} else {
//If we have not foumd the node with the correct value, we will look for the correct child note and look there:
if(this.value < value) {
if (rightTree != null) rightTree.deleteValue(value);
} else {
if (leftTree != null) leftTree.deleteValue(value);
}
}
return false;
}
public int getValue() {
return this.value;
}
public void relink(int i, SubTree t) {
if (i > 0) {
this.rightTree = t;
} else {
this.leftTree = t;
}
t.setNewParent(this);
}
public SubTree getChildNode(int i) {
if (i > 0) {
return this.rightTree;
} else {
return this.leftTree;
}
}
public void giveNewPlace(SubTree t) {
//Takes SubTree t and tries to give it a new place in the tree
//Check if this node has space for a left child node, if not:
//Check if this node has space for a right child node and order the two childnodes correct, if not:
//Ask the next left childNode to give new place with its giveNewPlace().
if (this.leftTree == null) {
this.leftTree = t;
t.setNewParent(this);
} else if (this.rightTree == null) {
if(getValue() < t.getValue()) {
this.rightTree = t;
t.setNewParent(this);
} else {
this.rightTree = this.leftTree;
this.leftTree = t;
t.setNewParent(this);
}
} else {
this.leftTree.giveNewPlace(t);
}
}
public void setNewParent(SubTree t) {
this.parent = t;
}
public void showObject() {
System.out.println("----------------------------------------");
if (parent != null) System.out.println("Parent: " + parent.getValue());
System.out.println("*Value: " + this.value);
if (rightTree != null) System.out.println("Right child: " + rightTree.getValue());
if (leftTree != null) System.out.println("Left child: " + leftTree.getValue());
System.out.println("----------------------------------------");
}
}
class BinarySeekingTree {
private SubTree rot;
public String toString() {
if (rot != null) {
return rot.toString();
} else {
return null;
}
}
public void insertValue(int value) {
if (rot != null) {
rot.insertValue(value);
} else {
rot = new SubTree(value, null);
}
}
public boolean deleteValue(int value) {
//If there is no root in the tree, then there is no value to delete
if (rot == null) {
return false;
} else {
if(rot.deleteValue(value)) {
return true;
} else {
return false;
}
}
}
public boolean lookForValue(int søkeVerdi) {
if (rot == null) {
return false;
}
return rot.lookForValue(søkeVerdi);
}
}
class Seek {
public static void main(String[] args) {
BinarySeekingTree tree = new BinarySeekingTree();
tree.insertValue(15);
tree.insertValue(10);
tree.insertValue(28);
tree.insertValue(3);
tree.insertValue(14);
tree.insertValue(20);
tree.insertValue(29);
tree.insertValue(1);
tree.insertValue(4);
tree.insertValue(12);
tree.insertValue(13);
tree.insertValue(16);
tree.insertValue(21);
tree.insertValue(30);
tree.insertValue(39);
System.out.println("The tree in a sorted display: " + tree.toString()); //Sorting fails after deleting an object
System.out.println("Is 3 in the tree: " + tree.lookForValue(3));
System.out.println("Is 4 in the tree: " + tree.lookForValue(4));
System.out.println("Is 1 in the tree: " + tree.lookForValue(1));
System.out.println("Is 10 in the tree: " + tree.lookForValue(10));
System.out.println("Is 12 in the tree: " + tree.lookForValue(12));
System.out.println("Is 13 in the tree: " + tree.lookForValue(13));
System.out.println("Is 14 in the tree: " + tree.lookForValue(14));
System.out.println("Is 16 in the tree: " + tree.lookForValue(16));
System.out.println("Is 20 in the tree: " + tree.lookForValue(20));
System.out.println("Is 21 in the tree: " + tree.lookForValue(21));
System.out.println("Is 28 in the tree: " + tree.lookForValue(28));
System.out.println("Is 29 in the tree: " + tree.lookForValue(29));
System.out.println("Is 30 in the tree: " + tree.lookForValue(30));
System.out.println("Is 39 in the tree: " + tree.lookForValue(39));
System.out.println("We now try to delete the value 10 from the tree, but not 28.");
tree.deleteValue(10);
//tree.deleteValue(28);
System.out.println("");
System.out.println("The tree in a sorted display: " + tree.toString()); //Sorting fails after deleting an object
System.out.println("Is 3 in the tree: " + tree.lookForValue(3));
System.out.println("Is 4 in the tree: " + tree.lookForValue(4));
System.out.println("Is 1 in the tree: " + tree.lookForValue(1));
System.out.println("Is 10 in the tree: " + tree.lookForValue(10));
System.out.println("Is 12 in the tree: " + tree.lookForValue(12));
System.out.println("Is 13 in the tree: " + tree.lookForValue(13));
System.out.println("Is 14 in the tree: " + tree.lookForValue(14));
System.out.println("Is 16 in the tree: " + tree.lookForValue(16));
System.out.println("Is 20 in the tree: " + tree.lookForValue(20));
System.out.println("Is 21 in the tree: " + tree.lookForValue(21));
System.out.println("Is 28 in the tree: " + tree.lookForValue(28));
System.out.println("Is 29 in the tree: " + tree.lookForValue(29));
System.out.println("Is 30 in the tree: " + tree.lookForValue(30));
System.out.println("Is 39 in the tree: " + tree.lookForValue(39));
}
}
SOLUTION
membership
This solution is only available to members.
To access this solution, you must be a member of Experts Exchange.
SOLUTION
membership
This solution is only available to members.
To access this solution, you must be a member of Experts Exchange.
ASKER CERTIFIED SOLUTION
membership
This solution is only available to members.
To access this solution, you must be a member of Experts Exchange.
Again, after removing the node 10 the left subtree should look like this:
4
/ \
3 14
/ /
1 12
\
13
This will solve both problems (1 and 2)
4
/ \
3 14
/ /
1 12
\
13
This will solve both problems (1 and 2)
SOLUTION
membership
This solution is only available to members.
To access this solution, you must be a member of Experts Exchange.
SOLUTION
membership
This solution is only available to members.
To access this solution, you must be a member of Experts Exchange.
ASKER
ioanton:
What you did was to rearrange the left side of the deleted node with the largest value at the top and attach it inplace of the deleted node. This works, but leads to what I guess would be a horrific bunch of code with plenty of complicated logic and algorithms. So I did it simpler. I re-wrote the code so that the left subtree gets passed to the root of the tree, without tempering with it. From there it is passed on as any other number and inserted where it is supposed to. The method giveNewPlace() was rewritten so that it takes in mind that the numbers should be larger or smaller then the parent node, not just larger on the right side compared to the left. All new nodes in the tree also keep track of what object is the root of the tree, so that they know where to pass they'r detached subtrees.
I included the changes that sailingbye suggested, and also added some of my own.
The result now looks like this after deleting 10:
The tree in a sorted display: 1 3 4 12 13 14 15 16 20 21 28 29 30 39
Is 3 in the tree: true
Is 4 in the tree: true
Is 1 in the tree: true
Is 10 in the tree: false
Is 12 in the tree: true
Is 13 in the tree: true
Is 14 in the tree: true
Is 16 in the tree: true
Is 20 in the tree: true
Is 21 in the tree: true
Is 28 in the tree: true
Is 29 in the tree: true
Is 30 in the tree: true
Is 39 in the tree: true
Looks all ok! Thanks for help!
What you did was to rearrange the left side of the deleted node with the largest value at the top and attach it inplace of the deleted node. This works, but leads to what I guess would be a horrific bunch of code with plenty of complicated logic and algorithms. So I did it simpler. I re-wrote the code so that the left subtree gets passed to the root of the tree, without tempering with it. From there it is passed on as any other number and inserted where it is supposed to. The method giveNewPlace() was rewritten so that it takes in mind that the numbers should be larger or smaller then the parent node, not just larger on the right side compared to the left. All new nodes in the tree also keep track of what object is the root of the tree, so that they know where to pass they'r detached subtrees.
I included the changes that sailingbye suggested, and also added some of my own.
The result now looks like this after deleting 10:
The tree in a sorted display: 1 3 4 12 13 14 15 16 20 21 28 29 30 39
Is 3 in the tree: true
Is 4 in the tree: true
Is 1 in the tree: true
Is 10 in the tree: false
Is 12 in the tree: true
Is 13 in the tree: true
Is 14 in the tree: true
Is 16 in the tree: true
Is 20 in the tree: true
Is 21 in the tree: true
Is 28 in the tree: true
Is 29 in the tree: true
Is 30 in the tree: true
Is 39 in the tree: true
Looks all ok! Thanks for help!
class SubTree {
private SubTree rightTree = null;
private SubTree leftTree = null;
private SubTree parent = null;
private SubTree root = null;
private int value = 0;
public SubTree(int value) {
this.value = value;
}
//This constructor is only used once, when the root is created. The root of the does not refer to any other root then itself.
public SubTree(int value, SubTree parent) {
this.value = value;
this.parent = parent;
this.root = this;
}
public SubTree(int value, SubTree parent, SubTree root) {
this.value = value;
this.parent = parent;
this.root = root;
}
public void insertValue(int newValue) {
if (value >= newValue) {
if (leftTree != null) {
leftTree.insertValue(newValue);
} else {
leftTree = new SubTree(newValue, this, root);
}
} else {
if (rightTree != null) {
rightTree.insertValue(newValue);
} else {
rightTree = new SubTree(newValue, this, root);
}
}
}
public String toString () {
String returString = "";
if (leftTree != null) {
returString = leftTree.toString() + " ";
}
returString = returString + value;
if (rightTree != null) {
returString = returString + " " + rightTree.toString();
}
showObject();
return returString;
}
public boolean lookForValue(int søkeVerdi) {
if (søkeVerdi == value) {
return true;
}
if (value > søkeVerdi) {
if (leftTree != null) {
return leftTree.lookForValue(søkeVerdi);
} else {
return false;
}
} else {
if (rightTree != null) {
return rightTree.lookForValue(søkeVerdi);
} else {
return false;
}
}
}
public boolean deleteValue(int value) {
if (this.value == value) {
//If we have found node with right value, we have to find if it has any child nodes
if ((rightTree == null) && (leftTree == null)) {
/**This node has no child, it can be linked off the tree.*/
if(value <= this.parent.getValue()) {
//We are on left side, and we will relink there at the parent
this.parent.relink(0, null);
} else { //We are on the right side, and we relink there at the parent
this.parent.relink(1, null);
}
//At the end we relink this objects backreference to parent:
this.parent = null;
return true;
} else if ((leftTree == null) || (rightTree == null)) {
/**The node has only one child node. We link over this node to the child */
if(value <= this.parent.getValue()) {
//We are on left side, and we link there over this object to this objects rightTree
if (leftTree == null) { this.parent.leftTree = this.rightTree; this.rightTree.setNewParent(this.parent); }
else { this.parent.leftTree = this.leftTree; this.leftTree.setNewParent(this.parent); }
} else {
//Or else we are on the right side, and we link there over this object to this objects leftTree
if (leftTree == null) { this.parent.rightTree = this.rightTree; this.rightTree.setNewParent(this.parent); }
else { this.parent.rightTree = this.leftTree; this.leftTree.setNewParent(this.parent); }
}
return true;
} else {
/**The noden has two child nodes, these have to moved correctly and placed correctly under the parent node */
if(value <= this.parent.getValue()) {
//We are on the left side, we link right child node on left side at the parent
//We then ask the right child node to find new space for the left childnode
this.parent.leftTree = this.rightTree;
this.rightTree.setNewParent(this.parent);
//this.rightTree.giveNewPlace(this.leftTree);
root.giveNewPlace(this.leftTree);
} else {
//Or else we are on the right side, and we link right child node on the right side at the parent
this.parent.rightTree = this.rightTree;
this.rightTree.setNewParent(this.parent);
//this.rightTree.giveNewPlace(this.leftTree);
root.giveNewPlace(this.leftTree);
}
return true;
}
} else {
//If we have not found the node with the correct value, we will look for the correct child note and look there:
if(this.value < value) {
if (rightTree != null) return rightTree.deleteValue(value);
} else {
if (leftTree != null) return leftTree.deleteValue(value);
}
}
return false;
}
public int getValue() {
return this.value;
}
public void relink(int i, SubTree t) {
if (i > 0) {
this.rightTree = t;
} else {
this.leftTree = t;
}
t.setNewParent(this);
}
public SubTree getChildNode(int i) {
if (i > 0) {
return this.rightTree;
} else {
return this.leftTree;
}
}
public void giveNewPlace(SubTree t) {
//Takes SubTree t and tries to give it a new place in the tree
//Check if this node has space for a left child node and that the coming child node is smaller then the to become parent, if not:
//Check if this node has space for a right child node and that the coming child node is larger then the to become parent, if not:
//If the becomming child node is smaller then the would be becomming parent, ask the next left childNode to give new place with its giveNewPlace().
//If the becomming child node is larger then the would be becomming parent, ask the next right childNode to give new place with its giveNewPlace().
if (this.leftTree == null && t.getValue() < getValue()) {
this.leftTree = t;
t.setNewParent(this);
} else if (this.rightTree == null && t.getValue() > getValue()) {
this.rightTree = t;
t.setNewParent(this);
} else {
if (t.getValue() < getValue()) this.leftTree.giveNewPlace(t);
if (t.getValue() > getValue()) this.rightTree.giveNewPlace(t);
}
}
public void setNewParent(SubTree t) {
this.parent = t;
}
public void showObject() {
System.out.println("----------------------------------------");
if (parent != null) System.out.println("Parent: " + parent.getValue());
System.out.println("*Value: " + this.value);
if (rightTree != null) System.out.println("Right child: " + rightTree.getValue());
if (leftTree != null) System.out.println("Left child: " + leftTree.getValue());
System.out.println("----------------------------------------");
}
}
class BinarySeekingTree {
private SubTree root;
public String toString() {
if (root != null) {
return root.toString();
} else {
return null;
}
}
public void insertValue(int value) {
if (root != null) {
root.insertValue(value);
} else {
root = new SubTree(value, null);
}
}
public boolean deleteValue(int value) {
//If there is no root in the tree, then there is no value to delete
if (root == null) {
return false;
} else {
if(root.deleteValue(value)) {
return true;
} else {
return false;
}
}
}
public boolean lookForValue(int søkeVerdi) {
if (root == null) {
return false;
}
return root.lookForValue(søkeVerdi);
}
}
class Seek {
public static void main(String[] args) {
BinarySeekingTree tree = new BinarySeekingTree();
tree.insertValue(15);
tree.insertValue(10);
tree.insertValue(28);
tree.insertValue(3);
tree.insertValue(14);
tree.insertValue(20);
tree.insertValue(29);
tree.insertValue(1);
tree.insertValue(4);
tree.insertValue(12);
tree.insertValue(13);
tree.insertValue(16);
tree.insertValue(21);
tree.insertValue(30);
tree.insertValue(39);
System.out.println("The tree in a sorted display: " + tree.toString()); //Sorting fails after deleting an object
System.out.println("Is 3 in the tree: " + tree.lookForValue(3));
System.out.println("Is 4 in the tree: " + tree.lookForValue(4));
System.out.println("Is 1 in the tree: " + tree.lookForValue(1));
System.out.println("Is 10 in the tree: " + tree.lookForValue(10));
System.out.println("Is 12 in the tree: " + tree.lookForValue(12));
System.out.println("Is 13 in the tree: " + tree.lookForValue(13));
System.out.println("Is 14 in the tree: " + tree.lookForValue(14));
System.out.println("Is 16 in the tree: " + tree.lookForValue(16));
System.out.println("Is 20 in the tree: " + tree.lookForValue(20));
System.out.println("Is 21 in the tree: " + tree.lookForValue(21));
System.out.println("Is 28 in the tree: " + tree.lookForValue(28));
System.out.println("Is 29 in the tree: " + tree.lookForValue(29));
System.out.println("Is 30 in the tree: " + tree.lookForValue(30));
System.out.println("Is 39 in the tree: " + tree.lookForValue(39));
System.out.println("We now try to delete the value 10 from the tree, but not 28.");
tree.deleteValue(10);
//tree.deleteValue(28);
System.out.println("");
System.out.println("The tree in a sorted display: " + tree.toString()); //Sorting fails after deleting an object
System.out.println("Is 3 in the tree: " + tree.lookForValue(3));
System.out.println("Is 4 in the tree: " + tree.lookForValue(4));
System.out.println("Is 1 in the tree: " + tree.lookForValue(1));
System.out.println("Is 10 in the tree: " + tree.lookForValue(10));
System.out.println("Is 12 in the tree: " + tree.lookForValue(12));
System.out.println("Is 13 in the tree: " + tree.lookForValue(13));
System.out.println("Is 14 in the tree: " + tree.lookForValue(14));
System.out.println("Is 16 in the tree: " + tree.lookForValue(16));
System.out.println("Is 20 in the tree: " + tree.lookForValue(20));
System.out.println("Is 21 in the tree: " + tree.lookForValue(21));
System.out.println("Is 28 in the tree: " + tree.lookForValue(28));
System.out.println("Is 29 in the tree: " + tree.lookForValue(29));
System.out.println("Is 30 in the tree: " + tree.lookForValue(30));
System.out.println("Is 39 in the tree: " + tree.lookForValue(39));
}
}ASKER
Please continue to comment if you have more suggestions.
It is possible to create more concise tree implementations but you have a recursive binary tree structure, the code is clear and understandable and above all it is correct for the given input. If I were you, to polish it off, I would add some a Javadoc comment to the beginning of each method. Otherwise, it's a job well done.
Regards
Regards
ASKER
ioanton: Yes, I agree. But I still don't understand why 1) and 2) occur as they do. I will try to rewrite the code as suggested here in this thread.