Mulitple Intersecting Calendar Appointment Drawing (Drawing Position Calculation of Appointments with overlapping times)
This is a bit of a hard one for me to explain, but here goes...
I am storing calendar appointments in a database for multiple people and I need to draw these together in a group view programmatically..
I am drawing the appointments on a page where time is from top to bottom.. eg. 8am is up the top and 8pm is down the bottom...
I have no trouble in calculating the y positions, the issue comes with the x positions if there are multiple appointments at the same time... I am drawing a separate box for each appointment...
The issue is such, when two or more appointments overlap how do I calculate (a) the width of the appointment box, and (b) it's starting x position.
The calculations I am currently doing work in the following scenarios
1) there are no overlapping of appointment times
2) there is only one overlap
3) there are any number of overlaps, but if there are more than one, then the others also overlap with all the ones currently overlapping and not just one of them.
Basically what I am doing at the moment is as follows:
1) Calculate the number of appointments an appointment intersects with
2) Divide the width specified for a day by this number to determine the single width for an appointment.
3) Keep a count of which number this appointment is relative to all the intersections to determine its starting x position.
This works perfectly fine for any number of appointments and "a certain type of intersection"
To explain my problem better I have attached 3 pictures...
The first two are generated by my code, and the last one has been modified in paint on how i want it to work...
The first picture explains what I mean that it works the way I want if the intersecting appointments intersect with all the other appointments in the same "section".
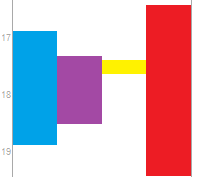
The second picture explains the problem I am having when I introduce an appointment that only intersects with one other appointment that is part of the section of intersections... it throws off the width of the existing appointments, the width of the new appointment is wrong, and the x position of the new appointment is way off.. [the appointment is being drawn with not the width i want and two days off to the right.. this is the flaw with my algorithm :)]

The following picture has been modified by me in a paint program. This is how I want the second picture to look.

Basically I want to know if there are any algorithms out there that will calculate the correct position no matter the type of intersections...
Outlook 2007 does it quite well, so there must be a way :)
I am storing calendar appointments in a database for multiple people and I need to draw these together in a group view programmatically..
I am drawing the appointments on a page where time is from top to bottom.. eg. 8am is up the top and 8pm is down the bottom...
I have no trouble in calculating the y positions, the issue comes with the x positions if there are multiple appointments at the same time... I am drawing a separate box for each appointment...
The issue is such, when two or more appointments overlap how do I calculate (a) the width of the appointment box, and (b) it's starting x position.
The calculations I am currently doing work in the following scenarios
1) there are no overlapping of appointment times
2) there is only one overlap
3) there are any number of overlaps, but if there are more than one, then the others also overlap with all the ones currently overlapping and not just one of them.
Basically what I am doing at the moment is as follows:
1) Calculate the number of appointments an appointment intersects with
2) Divide the width specified for a day by this number to determine the single width for an appointment.
3) Keep a count of which number this appointment is relative to all the intersections to determine its starting x position.
This works perfectly fine for any number of appointments and "a certain type of intersection"
To explain my problem better I have attached 3 pictures...
The first two are generated by my code, and the last one has been modified in paint on how i want it to work...
The first picture explains what I mean that it works the way I want if the intersecting appointments intersect with all the other appointments in the same "section".

The second picture explains the problem I am having when I introduce an appointment that only intersects with one other appointment that is part of the section of intersections... it throws off the width of the existing appointments, the width of the new appointment is wrong, and the x position of the new appointment is way off.. [the appointment is being drawn with not the width i want and two days off to the right.. this is the flaw with my algorithm :)]

The following picture has been modified by me in a paint program. This is how I want the second picture to look.

Basically I want to know if there are any algorithms out there that will calculate the correct position no matter the type of intersections...
Outlook 2007 does it quite well, so there must be a way :)
ASKER
Hi Fred, in the second picture the blue, purple, and the yellow stay the same... but the red now has 5 intersections, so it's width is modified, and its x position changes (making the yellow look smaller) because it think it's 4th in the progression of 5 appointments... the green is half the width of a day because it only intersects with one other appointment, and it is 2 days to the right because it thinks it is 5th in the progression of 5 appointmetns that are half the width of a day each.. (the counting in the code is a bit stuffed up when these scenarios happen)
Basically I think I will need a complete new algorithm to make it work the way I want.
Basically I think I will need a complete new algorithm to make it work the way I want.
Take a look at Interval Trees to see if that is of interest to you.
http://en.wikipedia.org/wiki/Interval_tree
If so, then here is a 50 minute video lecture (but much is just a proof of correctness). See Interval Trees starting at 36:15
http://academicearth.org/lectures/augmenting-data-structures-
http://en.wikipedia.org/wiki/Interval_tree
If so, then here is a 50 minute video lecture (but much is just a proof of correctness). See Interval Trees starting at 36:15
http://academicearth.org/lectures/augmenting-data-structures-
ASKER
Hi phoffric, I had a brief look and will have a more indepth one very soon...
But from what I can gather, Interval Trees are a process of determining the intervals that overlap?
I don't seem to have an issue with doing this by a brute force method, and am already successfully able to determine what intervals overlap with each other.
My problem arises when I go to draw these intervals that do overlap... How do I do it in the fashion described in my above question...
I'm not too sure how much you know about Interval Trees, but do you think this will solve that particular issue?
But from what I can gather, Interval Trees are a process of determining the intervals that overlap?
I don't seem to have an issue with doing this by a brute force method, and am already successfully able to determine what intervals overlap with each other.
My problem arises when I go to draw these intervals that do overlap... How do I do it in the fashion described in my above question...
I'm not too sure how much you know about Interval Trees, but do you think this will solve that particular issue?
I wasn't perfectly clear on your requirements, and I was hoping that perhaps the Interval Tree would help. Since it did not come to you as a solution, then I'd like to get on the same page w.r.t. your requirements. Here is my understanding of your requirements. I make all statements as a strawman requirement for you verification and clarification.
1. The y-axis is very clear from your description.
2. I gather that the x-axis is in units of days, and the width of each day is constant. And you have to fit in all the tasks that go into a single day.
3. Could you clarify how you define the schedule for a task? I know it has a start/stop time, but can it span multiple days (and if so, do the start/stop times change for each day?).
-- It would be helpful if you could provide an actual tabulation of the 5 tasks just to make sure we are on the same page.
4. Could you clarify why do you want the width to be different for each task. (You discussed how you implemented the width calculation; but it would be helpful if you could explain the requirement for the width.)
5. Re: width, in your good2.png image, why couldn't the 5 tasks in the first day all have the same width? What would be wrong if the green bar did not touch the red bar? What exactly does a wide width convey to the reader in a presentation?
6: Re: x-starting position, I realize that this is tied in to the width calculation; but if there are 5 tasks in one day and there is no overlap, then the x-position for each task, I guess would be 0 (in the first day). For two overlaps, I guess you would divide the day in half, so that one starts at 0, and the other starts at .5 (where .5 being halfway of the width allocated for one day). And if you had 5 tasks that all mutually overlapped, I guess then the day would be divided into 5 intervals, all evenly spaced along the x-axis.
7. In good2.png the five tasks are not mutually overlapped. Green/Red have an overlap depth of 2; whereas, Blue/Purple/Yellow/Red are mutually overlapping, and have an overlap depth of 4. So, I guess, in this case, you want to divide the day into 4 evenly spaced intervals for the day.
8. So, in general, if you have N tasks in one day, and if you consider all the different sets that are mutually overlapping sets, then the one set that has the maximum number of mutually overlapping tasks represents the number of intervals for the day. And from this number, the task x-start position and the width is trivial to compute. Here is where I intuitively thought that the depth of an Interval Tree may be useful, but I'll review it once I better understand your requirements.
9. re: The x-position of the tasks - Is it required that the Red be on the right? For a set of tasks, is there any reason it couldn't be on the left. It starts the earliest in the day, and has the longest duration, so that would look nicer IMO. But this is tied in to what exactly is the meaning of the x-position for a task. If Red could be on the left, then a natural ordering would be to sort on the primary key of start time, and the secondary key of stop time.
1. The y-axis is very clear from your description.
2. I gather that the x-axis is in units of days, and the width of each day is constant. And you have to fit in all the tasks that go into a single day.
3. Could you clarify how you define the schedule for a task? I know it has a start/stop time, but can it span multiple days (and if so, do the start/stop times change for each day?).
-- It would be helpful if you could provide an actual tabulation of the 5 tasks just to make sure we are on the same page.
4. Could you clarify why do you want the width to be different for each task. (You discussed how you implemented the width calculation; but it would be helpful if you could explain the requirement for the width.)
5. Re: width, in your good2.png image, why couldn't the 5 tasks in the first day all have the same width? What would be wrong if the green bar did not touch the red bar? What exactly does a wide width convey to the reader in a presentation?
6: Re: x-starting position, I realize that this is tied in to the width calculation; but if there are 5 tasks in one day and there is no overlap, then the x-position for each task, I guess would be 0 (in the first day). For two overlaps, I guess you would divide the day in half, so that one starts at 0, and the other starts at .5 (where .5 being halfway of the width allocated for one day). And if you had 5 tasks that all mutually overlapped, I guess then the day would be divided into 5 intervals, all evenly spaced along the x-axis.
7. In good2.png the five tasks are not mutually overlapped. Green/Red have an overlap depth of 2; whereas, Blue/Purple/Yellow/Red are mutually overlapping, and have an overlap depth of 4. So, I guess, in this case, you want to divide the day into 4 evenly spaced intervals for the day.
8. So, in general, if you have N tasks in one day, and if you consider all the different sets that are mutually overlapping sets, then the one set that has the maximum number of mutually overlapping tasks represents the number of intervals for the day. And from this number, the task x-start position and the width is trivial to compute. Here is where I intuitively thought that the depth of an Interval Tree may be useful, but I'll review it once I better understand your requirements.
9. re: The x-position of the tasks - Is it required that the Red be on the right? For a set of tasks, is there any reason it couldn't be on the left. It starts the earliest in the day, and has the longest duration, so that would look nicer IMO. But this is tied in to what exactly is the meaning of the x-position for a task. If Red could be on the left, then a natural ordering would be to sort on the primary key of start time, and the secondary key of stop time.
I forgot to add that at this point, I'd like to stick to your requirements and not how you implemented it. I'll be back tonight to continue this discussion.
ASKER CERTIFIED SOLUTION
membership
This solution is only available to members.
To access this solution, you must be a member of Experts Exchange.
ASKER
Hi phoffric...
[2. I gather that the x-axis is in units of days, and the width of each day is constant. And you have to fit in all the tasks that go into a single day.]
Yes this is correct.. (the width of each day can change, but only if the user resizes the window.. so in relation to the problem it is constant)
[3. Could you clarify how you define the schedule for a task? I know it has a start/stop time, but can it span multiple days (and if so, do the start/stop times change for each day?).
-- It would be helpful if you could provide an actual tabulation of the 5 tasks just to make sure we are on the same page.]
No spanning between mulitple days.. We are only concerned with apointments that are between the hours of 8am and 8pm. (your list of appointment times in your later post is fine)
[4. Could you clarify why do you want the width to be different for each task. (You discussed how you implemented the width calculation; but it would be helpful if you could explain the requirement for the width.)]
There is no requirement for width as such, all that is required is that overlapping appointments are drawn neatly within the width for a day.
[5. Re: width, in your good2.png image, why couldn't the 5 tasks in the first day all have the same width? What would be wrong if the green bar did not touch the red bar? What exactly does a wide width convey to the reader in a presentation?]
Width conveys no meaning, it is just for presentation.
It would be fine if they were all of the same width... the only reason the green bar is wider is because the space is there, and there will be a bit of text drawn on top of them, so the more horizontal realestate to draw on the better... but this is not a compulsary requirement..
[6: Re: x-starting position, I realize that this is tied in to the width calculation; but if there are 5 tasks in one day and there is no overlap, then the x-position for each task, I guess would be 0 (in the first day). For two overlaps, I guess you would divide the day in half, so that one starts at 0, and the other starts at .5 (where .5 being halfway of the width allocated for one day). And if you had 5 tasks that all mutually overlapped, I guess then the day would be divided into 5 intervals, all evenly spaced along the x-axis.]
Correct
[7. In good2.png the five tasks are not mutually overlapped. Green/Red have an overlap depth of 2; whereas, Blue/Purple/Yellow/Red are mutually overlapping, and have an overlap depth of 4. So, I guess, in this case, you want to divide the day into 4 evenly spaced intervals for the day.]
Correct
[8. So, in general, if you have N tasks in one day, and if you consider all the different sets that are mutually overlapping sets, then the one set that has the maximum number of mutually overlapping tasks represents the number of intervals for the day. And from this number, the task x-start position and the width is trivial to compute. Here is where I intuitively thought that the depth of an Interval Tree may be useful, but I'll review it once I better understand your requirements.]
This sounds fine, except if there was another appointment in the example that was earlier in the day that had no overlaps then I would really want this to span the whole width for the day.. and not be the same size as the appointments of the maximum number of mutually overlapping tasks. Would this be possible you think? Also if this appointment overlapped with another, and both of those did not overlap with anything else I would want them to take up half of the day width each if possible and not be limited to the size given to the appointments of the maximum numbber of mutualy overlapping tasks...
[9. re: The x-position of the tasks - Is it required that the Red be on the right? For a set of tasks, is there any reason it couldn't be on the left. It starts the earliest in the day, and has the longest duration, so that would look nicer IMO. But this is tied in to what exactly is the meaning of the x-position for a task. If Red could be on the left, then a natural ordering would be to sort on the primary key of start time, and the secondary key of stop time.]
Red can be on the left... The ordering of appointments from left to right has no underlying meaning, so they can be placed whereever is best for natural ordering.
[2. I gather that the x-axis is in units of days, and the width of each day is constant. And you have to fit in all the tasks that go into a single day.]
Yes this is correct.. (the width of each day can change, but only if the user resizes the window.. so in relation to the problem it is constant)
[3. Could you clarify how you define the schedule for a task? I know it has a start/stop time, but can it span multiple days (and if so, do the start/stop times change for each day?).
-- It would be helpful if you could provide an actual tabulation of the 5 tasks just to make sure we are on the same page.]
No spanning between mulitple days.. We are only concerned with apointments that are between the hours of 8am and 8pm. (your list of appointment times in your later post is fine)
[4. Could you clarify why do you want the width to be different for each task. (You discussed how you implemented the width calculation; but it would be helpful if you could explain the requirement for the width.)]
There is no requirement for width as such, all that is required is that overlapping appointments are drawn neatly within the width for a day.
[5. Re: width, in your good2.png image, why couldn't the 5 tasks in the first day all have the same width? What would be wrong if the green bar did not touch the red bar? What exactly does a wide width convey to the reader in a presentation?]
Width conveys no meaning, it is just for presentation.
It would be fine if they were all of the same width... the only reason the green bar is wider is because the space is there, and there will be a bit of text drawn on top of them, so the more horizontal realestate to draw on the better... but this is not a compulsary requirement..
[6: Re: x-starting position, I realize that this is tied in to the width calculation; but if there are 5 tasks in one day and there is no overlap, then the x-position for each task, I guess would be 0 (in the first day). For two overlaps, I guess you would divide the day in half, so that one starts at 0, and the other starts at .5 (where .5 being halfway of the width allocated for one day). And if you had 5 tasks that all mutually overlapped, I guess then the day would be divided into 5 intervals, all evenly spaced along the x-axis.]
Correct
[7. In good2.png the five tasks are not mutually overlapped. Green/Red have an overlap depth of 2; whereas, Blue/Purple/Yellow/Red are mutually overlapping, and have an overlap depth of 4. So, I guess, in this case, you want to divide the day into 4 evenly spaced intervals for the day.]
Correct
[8. So, in general, if you have N tasks in one day, and if you consider all the different sets that are mutually overlapping sets, then the one set that has the maximum number of mutually overlapping tasks represents the number of intervals for the day. And from this number, the task x-start position and the width is trivial to compute. Here is where I intuitively thought that the depth of an Interval Tree may be useful, but I'll review it once I better understand your requirements.]
This sounds fine, except if there was another appointment in the example that was earlier in the day that had no overlaps then I would really want this to span the whole width for the day.. and not be the same size as the appointments of the maximum number of mutually overlapping tasks. Would this be possible you think? Also if this appointment overlapped with another, and both of those did not overlap with anything else I would want them to take up half of the day width each if possible and not be limited to the size given to the appointments of the maximum numbber of mutualy overlapping tasks...
[9. re: The x-position of the tasks - Is it required that the Red be on the right? For a set of tasks, is there any reason it couldn't be on the left. It starts the earliest in the day, and has the longest duration, so that would look nicer IMO. But this is tied in to what exactly is the meaning of the x-position for a task. If Red could be on the left, then a natural ordering would be to sort on the primary key of start time, and the secondary key of stop time.]
Red can be on the left... The ordering of appointments from left to right has no underlying meaning, so they can be placed whereever is best for natural ordering.
The simplest approach is to use the matrix in http:#33685331. Do you see any issues with using this method? Again, this approach requires fixed lengths bins. Even if the start/stop times were minute based, that still does not result in too many columns (60 * 12).
>> ... another appointment ... was earlier in the day that had no overlaps then ... to span the whole width for the day.
I don't see any problem with this requirement. The matrix can be used here as well.
>> if this appointment overlapped with another, and both of those did not overlap with anything else I would want them to take up half of the day width each
I don't see any problem with this requirement. If we represented the tasks in a graph, then these two nodes would not be connected to the others. For each disjoint set, compute the maximum numbber of mutualy overlapping tasks and set the task width for that disjoint set accordingly.
The matrix can be used here as well.
>> ... another appointment ... was earlier in the day that had no overlaps then ... to span the whole width for the day.
I don't see any problem with this requirement. The matrix can be used here as well.
>> if this appointment overlapped with another, and both of those did not overlap with anything else I would want them to take up half of the day width each
I don't see any problem with this requirement. If we represented the tasks in a graph, then these two nodes would not be connected to the others. For each disjoint set, compute the maximum numbber of mutualy overlapping tasks and set the task width for that disjoint set accordingly.
The matrix can be used here as well.
ASKER
Thanks phoffric...
I'm working through an example on paper right now with the method you have outlined in 33685331...
I'll let you know how it goes..
I'll reply again soon after I've gone through an example... I think there might be one more case that I would like to accomodate, but I won't know for sure until I go through it on paper...
I'm working through an example on paper right now with the method you have outlined in 33685331...
I'll let you know how it goes..
I'll reply again soon after I've gone through an example... I think there might be one more case that I would like to accomodate, but I won't know for sure until I go through it on paper...
Using the matrix, after identifying the disjoint sets into their own regions along the horizontal axis, and then collapsing the regions independently of the others (as shown in the second matrix - i.e., reducing the number of rows), then the empty cells in the matrix below (or above, depending upon how you organize your data - any organization is fine, I think) become available for color-filling.
ASKER
Hi phoffric
I just went through an example on paper with the bins and they work good...
I'm going to code it up now, should be finished by the end of day (it's 11:30AM here at the moment)...
I'll let you know how I go...
I'm going to start off with the simple case, and then introduce the graphs for the disjointed sets...
Another question if I may, relating to space filling for non-disjointed appointments. if we take your example in "33685331",
==========================
2xxxxxxxxxxxxxxxxxxxxxxxxx
1x 3xxxxxxxxxxxxxxxxxx
4xxxxxxxxxx
5x 6xx
==========================
can you see a method for letting appointment #1 know it can fill more space?
I've come up with a possibility which I will try out once I've implemented the method you have outlined..
Do you think this would work?
For the example:
Interval Width = Day Width / 4
Max Possible Width Mulitplier of Appointment = 4 - Max Appointment Intersections
Hence for all appoinments except appointment #1, their max possible width multiplier is 1, because on at least on part of their length they intersect with 3 other appointments,
eg. 4 - 3 = 1.
But for Appointment #1 it would be 4 - 1 = 3, because on any part of its length it has a max of 1 intersection.
It is fairly basic to check the gaps underneath each segment of appointment 1 to okay it to fill the appropriate space underneath it...
the issue is with an example like this, for appointment #7...
I think I have a way to handle this by first figuring out it's max width by starting with it's max possible width as defined above, seeing if it fits anywhere, if not then minus 1 from it and see if that fits anywhere, etc... , but can you see any problems with what I am attempting to do?
I hope I have explained it sufficiently.
==========================
2xxxxxxxxxxxxxxxxxxxxxxxxx
1x 3xxxxxxxx 7x
4xxxxxxxxxx
5x 6xx
8xxxx
==========================
As I said, I'll go ahead now and code up the solution in 33685331, I will then do the graph method for the disjointed sets... Then I will try and tackle this last issue, but if it can't be solved I doubt it will matter too much...
Thank you
I just went through an example on paper with the bins and they work good...
I'm going to code it up now, should be finished by the end of day (it's 11:30AM here at the moment)...
I'll let you know how I go...
I'm going to start off with the simple case, and then introduce the graphs for the disjointed sets...
Another question if I may, relating to space filling for non-disjointed appointments. if we take your example in "33685331",
==========================
2xxxxxxxxxxxxxxxxxxxxxxxxx
1x 3xxxxxxxxxxxxxxxxxx
4xxxxxxxxxx
5x 6xx
==========================
can you see a method for letting appointment #1 know it can fill more space?
I've come up with a possibility which I will try out once I've implemented the method you have outlined..
Do you think this would work?
For the example:
Interval Width = Day Width / 4
Max Possible Width Mulitplier of Appointment = 4 - Max Appointment Intersections
Hence for all appoinments except appointment #1, their max possible width multiplier is 1, because on at least on part of their length they intersect with 3 other appointments,
eg. 4 - 3 = 1.
But for Appointment #1 it would be 4 - 1 = 3, because on any part of its length it has a max of 1 intersection.
It is fairly basic to check the gaps underneath each segment of appointment 1 to okay it to fill the appropriate space underneath it...
the issue is with an example like this, for appointment #7...
I think I have a way to handle this by first figuring out it's max width by starting with it's max possible width as defined above, seeing if it fits anywhere, if not then minus 1 from it and see if that fits anywhere, etc... , but can you see any problems with what I am attempting to do?
I hope I have explained it sufficiently.
==========================
2xxxxxxxxxxxxxxxxxxxxxxxxx
1x 3xxxxxxxx 7x
4xxxxxxxxxx
5x 6xx
8xxxx
==========================
As I said, I'll go ahead now and code up the solution in 33685331, I will then do the graph method for the disjointed sets... Then I will try and tackle this last issue, but if it can't be solved I doubt it will matter too much...
Thank you
Re: your last example:
==========================
2xxxxxxxxxxxxxxxxxxxxxxxxx
1x 3xxxxxxxx 7x
4xxxxxxxxxx
5x 6xx
8xxxx
==========================
Rather than using formulas for color filling, I'd prefer a set approach. In this connected set of 8 tasks, you know to divide the day into 5 sections. You have no problem filling the first section with task 2. And you have no problem filling in the next row with 1's, 3's, and 7's.
Now look at the matrix throwing away (temporarily row 1). Now you see that there are two disjoint sets (task 1 is one, and other 6 tasks are the other). So, task 1 gets filled in for remaining columns:
Throw away row 2, and it is easy to fill in the 4's.
Then throw away row 3. So far we have:
==========================
2xxxxxxxxxxxxxxxxxxxxxxxxx
1x 3xxxxxxxx 7x
4xxxxxxxxxx
==========================
5x 6xx
8xxxx
==========================
21111
21111
2
23
23
234
234
234
234
234
2 4
274
274
2 4
2 4
2
2
2
Tasks 5 and 6 are not disjoint (connected by task 8), so they take up a width of 1 section. And I think you end up with this color coding:
21111
21111
2
23
23
234
234
234
234
23458
2 458
274 8
27468
2 468
2 46
2
2
2
I may be able to check back in 1-2 hours briefly, and definitely tomorrow.
==========================
2xxxxxxxxxxxxxxxxxxxxxxxxx
1x 3xxxxxxxx 7x
4xxxxxxxxxx
5x 6xx
8xxxx
==========================
Rather than using formulas for color filling, I'd prefer a set approach. In this connected set of 8 tasks, you know to divide the day into 5 sections. You have no problem filling the first section with task 2. And you have no problem filling in the next row with 1's, 3's, and 7's.
Now look at the matrix throwing away (temporarily row 1). Now you see that there are two disjoint sets (task 1 is one, and other 6 tasks are the other). So, task 1 gets filled in for remaining columns:
Throw away row 2, and it is easy to fill in the 4's.
Then throw away row 3. So far we have:
==========================
2xxxxxxxxxxxxxxxxxxxxxxxxx
1x 3xxxxxxxx 7x
4xxxxxxxxxx
==========================
5x 6xx
8xxxx
==========================
21111
21111
2
23
23
234
234
234
234
234
2 4
274
274
2 4
2 4
2
2
2
Tasks 5 and 6 are not disjoint (connected by task 8), so they take up a width of 1 section. And I think you end up with this color coding:
21111
21111
2
23
23
234
234
234
234
23458
2 458
274 8
27468
2 468
2 46
2
2
2
I may be able to check back in 1-2 hours briefly, and definitely tomorrow.
For a given matrix, you should also see what issues arise if your interchange the rows. This could be handled more formally with graphs, but the matrix seems to provide an easy approach (which is semi-graphical).
In the above approach, the color filling algorithm is one of non-overlapping sub-problems. First you give a non-disjoint set (i.e., all tasks mutually reachable in a graph) and figured out that there are 5 sections. After filling in the first section (at least internally - you can save the drawing for last if desired), then the next problem is filling in the remaining 4 sections (and you threw away the first row after making disjoint decisions on how many sets to deal with). Throwing away the first row resulted in two sub-problems (i.e., two disjoint sets) and they have to be dealt with individually, and in the same way as dealing with the original problem.
So, it appears that a recursive solution would work for the color-filling algorithm where at each step, you determine the number of disjoint sets and apply the color algorithm to each one of them. (I admit, I'm just winging it quickly on this point, since I have to go; but I'd at least think about this idea.)
So, it appears that a recursive solution would work for the color-filling algorithm where at each step, you determine the number of disjoint sets and apply the color algorithm to each one of them. (I admit, I'm just winging it quickly on this point, since I have to go; but I'd at least think about this idea.)
ASKER
terrific!
thanks phoffric, it worked!
I have only implemented the basic approach so far. I am still yet to do the graphs, and then the more complex sizing for the advanced color filling.
I have attached a picture of a group of appointments generated by the newley implemented solution...
I will go ahead and do the graphs in the morning, and then make an attempt at the advanced sizing...
Should I accept the solution now on here, or should wait until tomorrow after I make an attempt on the graphs for the disjoint sets?
excellent.png
thanks phoffric, it worked!
I have only implemented the basic approach so far. I am still yet to do the graphs, and then the more complex sizing for the advanced color filling.
I have attached a picture of a group of appointments generated by the newley implemented solution...
I will go ahead and do the graphs in the morning, and then make an attempt at the advanced sizing...
Should I accept the solution now on here, or should wait until tomorrow after I make an attempt on the graphs for the disjoint sets?
excellent.png
ASKER
PS... Ignore the white numbers on the appointments, they are simply referencing unrelated job ids.
just using them for testing out the drawing of some info..
just using them for testing out the drawing of some info..
Glad to see that you are on a good track. You can accept now if you think you got this question answered. If there is something wrong, then you can reopen the question, or ask a related question as appropriate.
What language and graphics package are you working with? Would you be interested in posting your code?
What language and graphics package are you working with? Would you be interested in posting your code?
ASKER
Hi phoffric...
I'm using C#, it's the standards graphics package built in.. I think it's GDI. I'm using Microsoft Visual Studio 2008...
I'll post my code up once I've cleaned it up, and put some comments in...
I'm trying to do the graphs and connected nodes at the moment to calculate the distinct sets, but I'm struggling on how to do this... I'm trying to figure out if recursion is the way to go, and if so how...
Is there a basic method to do this?
I'm using C#, it's the standards graphics package built in.. I think it's GDI. I'm using Microsoft Visual Studio 2008...
I'll post my code up once I've cleaned it up, and put some comments in...
I'm trying to do the graphs and connected nodes at the moment to calculate the distinct sets, but I'm struggling on how to do this... I'm trying to figure out if recursion is the way to go, and if so how...
Is there a basic method to do this?
ASKER
I got the graphs working now...
Because the appoinments are sorted by starttime, and length it was a fairly easy process...
Loop through the nodes...
if the node intersects with any nodes in the current distinct set then add it to the distinct set
if not, then create a new distinct set, add the node, and set it as the current distinct set
I'll clean up my code, do some commenting and post it up...
Only thing left for me to do is the advanced color filling...
Because the appoinments are sorted by starttime, and length it was a fairly easy process...
Loop through the nodes...
if the node intersects with any nodes in the current distinct set then add it to the distinct set
if not, then create a new distinct set, add the node, and set it as the current distinct set
I'll clean up my code, do some commenting and post it up...
Only thing left for me to do is the advanced color filling...
>> sorted by start-time, and length
Yes, usually some kind of sort generally helps simplify an algorithm.
Looks like you're doing good. I'm looking forwards to seeing your final results. If you have an approach that you are comfortable, then that is fine. In general, recursion is supposed to make programming easier (at some expense to performance). So, please do not try to force recursion as a solution unless required.
Yes, usually some kind of sort generally helps simplify an algorithm.
Looks like you're doing good. I'm looking forwards to seeing your final results. If you have an approach that you are comfortable, then that is fine. In general, recursion is supposed to make programming easier (at some expense to performance). So, please do not try to force recursion as a solution unless required.
ASKER
Thanks for all your help phoffric...
Everything is working...
The snippet contains the three major methods involved in the process...
Please note that there is additional code in one of the methods that divides each appointment up further if mulitple staff are assigned to the same appointment such that the appointment box can be filled with each persons colour.
First Method returns a list of distinct sets of calendar appointments from a list of calendar appoinments.
Second Method is a recursive method that processes a distinct set of appointments.
Third Method puts it all together.
Everything is working...
The snippet contains the three major methods involved in the process...
Please note that there is additional code in one of the methods that divides each appointment up further if mulitple staff are assigned to the same appointment such that the appointment box can be filled with each persons colour.
First Method returns a list of distinct sets of calendar appointments from a list of calendar appoinments.
Second Method is a recursive method that processes a distinct set of appointments.
Third Method puts it all together.
// return a list of distinct sets of calendarboxes
public static List<List<CalendarBox>> GetDistinctSets(List<CalendarBox> calendarBoxes)
{
// create the container for the list of distinct sets
List<List<CalendarBox>> distinctSetsCB = new List<List<CalendarBox>>();
if (calendarBoxes == null || calendarBoxes.Count == 0)
{
// if no input calendarBoxes then do nothing
}
else
{
// create a distinct list
distinctSetsCB.Add(new List<CalendarBox>());
// add the first calendar box
distinctSetsCB[0].Add(calendarBoxes[0]);
// Loop through the calendar boxes...
// if the calendar box intersects with a calendar box
// that is already part of the set then add
// it to the set... if no intersection is made
// then create a new distinct set, set it as current, and add
// the calendar box to it....
foreach (CalendarBox cb in calendarBoxes)
{
// The Current Distinct Set
List<CalendarBox> theDistinctSet = distinctSetsCB[distinctSetsCB.Count - 1];
bool noIntersections = true;
foreach (CalendarBox dsCB in theDistinctSet)
{
if (CalendarBox.Intersect(cb, dsCB))
{
// appointment intersects with a member of the distinct set
noIntersections = false;
}
}
if (noIntersections)
{
// No Intersection, so create a new distinct set (becomes the current) and add
// the calendar appointment to it
distinctSetsCB.Add(new List<CalendarBox>());
distinctSetsCB[distinctSetsCB.Count - 1].Add(cb);
}
else
{
// Intersection found, so add the appoinment to the current distinct set
if (!theDistinctSet.Contains(cb))
theDistinctSet.Add(cb);
}
}
}
return distinctSetsCB;
}
// process a distinct sets of calendar appointments
// recursive method
private void DoDistinctSet(List<CalendarBox> calendarBoxSet, float widthOffset)
{
int maxMatrixColumn = 0;
int[][] matrix = NewMatrix(matrixWidth, (int)(matrixCellsPerHour * 25f));
foreach (CalendarBox cb in calendarBoxSet)
{
int startCell = (int)(cb.hourStart * matrixCellsPerHour);
float endCellFloat = ((cb.hourEnd - 0.01f) * matrixCellsPerHour);
int endCell = (int)endCellFloat;
// if the appointment ends on the edge of a cell, then don't include that cell
if (endCellFloat - (float)((int)endCellFloat) < 0.001)
endCell = endCell - 1;
// Loop through the matrix columns, to find the first column
// where all of the appointment will fit...
int matrixColumnCount = -1;
bool okayToWrite = false;
while (!okayToWrite)
{
matrixColumnCount++;
okayToWrite = true;
for (int k = startCell; k <= endCell; k++)
{
if (matrix[matrixColumnCount][k] != 0)
okayToWrite = false;
}
}
// set the start cell and end cell for the appointment
// also set the matrix column it belongs to.
cb.StartCell = startCell;
cb.EndCell = endCell;
cb.MatrixColumn = matrixColumnCount;
// keep a record of the max column used
if (matrixColumnCount > maxMatrixColumn)
{
maxMatrixColumn = matrixColumnCount;
}
// fill in the matrix cells with the appointment id
for (int k = startCell; k <= endCell; k++)
{
matrix[matrixColumnCount][k] = cb.CalendarID;
}
}
// total number of matrix columns used
int totalMatrixColumns = maxMatrixColumn + 1;
// calculate the width of appointments for this distinct set.
float MaxTrixBoxWidth = ((dayWidth-widthOffset) / (float)totalMatrixColumns);
// set the xstart and xend positions of the calendar box.
foreach (CalendarBox cb in calendarBoxSet)
{
cb.XStart = cb.XDayStart + widthOffset + (float)cb.MatrixColumn * MaxTrixBoxWidth; //((dayWidth - widthOffset) / (float)totalMatrixColumns));
cb.XEnd = cb.XStart + MaxTrixBoxWidth;
}
// compute special filling width if number of columns is greater than two
// if 2 or 1 columns then the appointments will always be their max possible width
if (totalMatrixColumns > 2)
{
float newWidthOffset = MaxTrixBoxWidth + widthOffset;
// ignore the first column because its will never expand
// process the other columns for advanced filling of colour
// all calendar boxes except the first column
List<CalendarBox> otherCalBoxes = new List<CalendarBox>();
foreach (CalendarBox cb in calendarBoxSet)
{
if (cb.MatrixColumn > 0)
otherCalBoxes.Add(cb);
}
// get the distinct sets of the calendar boxes, ignoring the first row
List<List<CalendarBox>> distinctSets = CalendarBox.GetDistinctSets(otherCalBoxes);
foreach (List<CalendarBox> cBoxSet in distinctSets)
{
DoDistinctSet(cBoxSet, newWidthOffset);
}
}
}
// Draw the calendar from startDay, for a total of numberOfDays
private void DrawDays(DateTime startDay, int numberOfDays, Graphics g)
{
// The Width that each day has on the screen
dayWidth = (float)GetCalendarWidth() / (float)numberOfDays;
// The Height that each day has on the screen
hourHeight = (float)GetCalendarHeight() / (float)hoursDisplayed;
// The Calendar Boxes.. (used for mouse overs)
List<CalendarBox> TheCalendarBoxes = new List<CalendarBox>();
// Draw the Day Names / Date, and the veritcal day border lines.
for (int i = 0; i < numberOfDays; i++)
{
g.DrawString(startDay.AddDays(i).ToString("ddd, d MMM yyyy"), dayFont, dayBrush, new PointF(globalXOffset + dayStringXOffset + (float)i * dayWidth, dayStringYOffset));
g.DrawLine(dayBorderPen, new PointF(globalXOffset + (float)i * dayWidth, 0), new PointF(globalXOffset + (float)i * dayWidth, (float)panel1.Height));
}
// Draw the hours down the vertical line, right aligned.
int hourCount = 1;
StringFormat sf = new StringFormat();
sf.Alignment = StringAlignment.Far;
for (int i = startingHour+1; i < startingHour+hoursDisplayed; i++)
{
g.DrawString(i.ToString(), hourFont, hourBrush, new PointF(globalXOffset + hourStringXOffset, hourCount * hourHeight), sf);
hourCount++;
}
// this draws the calendar appointments
for (int i = 0; i < numberOfDays; i++)
{
// the loop goes through each day by day
// DateTimes of the day being currently drawn, and the next day for use in filter below
DateTime CurrentDrawingDate = StartDate.AddDays((int)nUPDownDays.Value * IntervalPosition).AddDays(i);
DateTime CurrentDrawingDateAddOne = CurrentDrawingDate.AddDays(1);
// SQL Friendly string representations of the above DateTimes
string currentDrawingDate = "'" + CurrentDrawingDate.Year.ToString() + "-" +
CurrentDrawingDate.Month.ToString() + "-" +
CurrentDrawingDate.Day.ToString() + "'";
string currentDrawingDateAddOne = "'" + CurrentDrawingDateAddOne.Year.ToString() + "-" +
CurrentDrawingDateAddOne.Month.ToString() + "-" +
CurrentDrawingDateAddOne.Day.ToString() + "'";
// Use the binding source filter such that only the appointments for the current day
// are available...
CalendarBindingSource.Filter = "(StartDateTime >= " + currentDrawingDate + " AND " +
"StartDateTime < " + currentDrawingDateAddOne + ")";
// Sort the results by Start Time, and Length of Appointment.
CalendarBindingSource.Sort = "StartDateTime ASC, TotalMinutes ASC";
// Loop through the calendar appointments for
// the day currently being drawn, and place them into CalendarBox container objects
List<CalendarBox> myCalendarBoxes = new List<CalendarBox>();
for (int j = 0; j < CalendarBindingSource.Count; j++)
{
// get the calendar row
CLD.JOBMANAGERDataSet.CalendarRow cr = (CLD.JOBMANAGERDataSet.CalendarRow)(((DataRowView)CalendarBindingSource[j]).Row);
// create a new calendar box from the calendar row
CalendarBox cb = new CalendarBox(cr);
// leftmost starting position for the current day
float xPosition = globalXOffset + (float)i * dayWidth;
// create a float of the start time and end time of the appoinment, in hours for that day.. (eg. 11:30 = 11.5)
float hoursStart = cr.StartDateTime.Hour + ((float)cr.StartDateTime.Minute / (float)60);
float hoursEnd = cr.EndDateTime.Hour + ((float)cr.EndDateTime.Minute / (float)60);
// adjust for the calendar starting hour offset
hoursStart = hoursStart - startingHour;
hoursEnd = hoursEnd - startingHour;
// calculate the start and end y position of the appointment
float yPosition = hoursStart * hourHeight;
float yPositionEnd = hoursEnd * hourHeight;
/// Appointments that span mulitple days are ignored, as they are not likely
/// in our environment...
///
/// If there is an appointment that does span, then it is handled by the following:
///
// if the appointment goes over multiple days then draw it to the bottom of the day
if (cr.EndDateTime.Day != cr.StartDateTime.Day)
yPositionEnd = panel1.Height;
// if the appointment goes over the bottom boundary, then draw it to the bottom of the day
if (yPositionEnd > panel1.Height)
yPositionEnd = panel1.Height;
cb.XDayStart = xPosition;
cb.XEnd = xPosition + dayWidth;
cb.YStart = yPosition;
cb.YEnd = yPositionEnd;
myCalendarBoxes.Add(cb);
}
// Get the distinct sets of calendar boxes...
List<List<CalendarBox>> distinctSetsCB = CalendarBox.GetDistinctSets(myCalendarBoxes);
foreach (List<CalendarBox> distincSetOfCalendarBoxes in distinctSetsCB)
{
DoDistinctSet(distincSetOfCalendarBoxes, 0f);
}
foreach (CalendarBox cb in myCalendarBoxes)
{
g.FillRectangle(scheduleBrush, cb.XStart, cb.YStart, cb.XEnd-cb.XStart, (cb.YEnd - cb.YStart));
if (cb.CalendarStaff != null)
{
int totalcount = cb.CalendarStaff.Count;
int count = 0;
float singleWidth = 0;
if (totalcount != 0)
{
singleWidth = (cb.XEnd-cb.XStart) / (float)totalcount;
}
foreach (CLD.JOBMANAGERDataSet.CalendarStaffRow csr in cb.CalendarStaff)
{
Brush myBrush = scheduleBrush;
if (!csr.IsStaffColourNull())
{
myBrush = new SolidBrush(Color.FromName(csr.StaffColour));
}
g.FillRectangle(myBrush, cb.XStart + count * singleWidth, cb.YStart, singleWidth, (cb.YEnd - cb.YStart));
count++;
}
}
g.DrawRectangle(calendarBorderPen, cb.XStart, cb.YStart, (cb.XEnd - cb.XStart), (cb.YEnd - cb.YStart));
g.DrawString("#" + cb.jobid.ToString(), calendarFont, calendarBrush, new PointF(cb.XStart, cb.YStart));
}
TheCalendarBoxes.AddRange(myCalendarBoxes);
}
this.TheCalendarBoxes = TheCalendarBoxes;
}
ASKER
forgot to select multiple solution, as further comments by the same expert gave additional info on how to achieve secondary goals... these can be gathered by reading all his posts in this question.
Also, code is provided below that implements the solution.
Also, code is provided below that implements the solution.
Glad to have helped. :)
If you run into any other specific schedules that don't fit nicely, you can post it here, and I'll take a look. Best of luck to you! Interesting problem.
I hope your listing will be useful to a C# person.
I'm a C/C++ programmer. I downloaded VS 2008 Express C#, ran through their web browser starter video. Then I plugged in your code in a new project to see what I could make out of it. But too many errors for me to decipher. Well maybe another day after I've learned C#, I'll be able to figure out what is necessary to make the program complete.
If you run into any other specific schedules that don't fit nicely, you can post it here, and I'll take a look. Best of luck to you! Interesting problem.
I hope your listing will be useful to a C# person.
I'm a C/C++ programmer. I downloaded VS 2008 Express C#, ran through their web browser starter video. Then I plugged in your code in a new project to see what I could make out of it. But too many errors for me to decipher. Well maybe another day after I've learned C#, I'll be able to figure out what is necessary to make the program complete.
ASKER
Unless you don't know C# it would be fairly difficult to wing it to get it working in C# :)
It's part of a very large piece of software that I can't really post up here....
When I get some time this weekend I'll create a stand alone project that only contains this Calendar and uses a built in datasource instead of linking it to SQL...
That way I can post the whole Visual Studio Project and you will be able to run it without modification...
It's part of a very large piece of software that I can't really post up here....
When I get some time this weekend I'll create a stand alone project that only contains this Calendar and uses a built in datasource instead of linking it to SQL...
That way I can post the whole Visual Studio Project and you will be able to run it without modification...
Thanks. FYI - EE checks zip files of projects and removes contents. I believe that if you change the extension from .zip to .txt, maybe that will bypass the filters. If you want to send me the project zipped up (see my profile), then I can see how to get a VS project uploaded.
ASKER
Okay, I've stripped the database stuff, and substituded in some hardcoded objects...
It's pretty messy, especially after I hacked together the non-database stuff... it might seem a bit weird..
It does the trick though...
Should work straight away... I've tested it on another PC and it worked good.
http://www.turbocharger-kit.com/CalendarSample.zip
Also, you may need to press back a couple of times in the program if you open this up in a couple of weeks or so as the appointments i've made are for the upcoming week... should be pretty easy to get the hang of it...
Also I've disabled the staff colours (as this was also database stuff), so all appointments will be the same colour so you might want to do some random colouring scheme to make it look a bit nicer..
Also some of the descriptive text will just say -1 or something...
Let me know how you go...
It's pretty messy, especially after I hacked together the non-database stuff... it might seem a bit weird..
It does the trick though...
Should work straight away... I've tested it on another PC and it worked good.
http://www.turbocharger-kit.com/CalendarSample.zip
Also, you may need to press back a couple of times in the program if you open this up in a couple of weeks or so as the appointments i've made are for the upcoming week... should be pretty easy to get the hang of it...
Also I've disabled the staff colours (as this was also database stuff), so all appointments will be the same colour so you might want to do some random colouring scheme to make it look a bit nicer..
Also some of the descriptive text will just say -1 or something...
Let me know how you go...
Thanks for posting! This truly adds completion to this question. :)
Without knowing the C# details, I'd say your program is pretty nice. Looks like you are taking advantage of C# standard library so as to not reinvent the wheel.
I'm probably not the person to critique, but I'll give a stab. (If interested in pursuing a critique from C# experts, by all means ask a related question and get a code/design review.) Here goes..
A method to get data should be in separate file. In your real version, this would have all the SQL code methods in one file. When calling the primary api, your data structures are now completely filled. (In large development systems, then other developers can stub out the method replacing with hard-coded dummy data, as you did. With this design approach, the code does not get messy when stubbing.
All the algorithmic methods discussed in this question should be in a separate file. The input is the data structures that were filled by the method to get data. This algorithmic class produces results in data structures that are related to this question.
Then these algorithmic results are sent to a graphics builder (possibly a separate file), and its results are sent to the view rendering methods, a separate file.
Breaking this program into at least three separate files (get data, algorithmic analysis, graphics view) lends itself to a clean design allowing for each class to be tested independently of the other classes.
I'll try to find time to learn C# by February. This will be my first project! Thanks again.
Without knowing the C# details, I'd say your program is pretty nice. Looks like you are taking advantage of C# standard library so as to not reinvent the wheel.
I'm probably not the person to critique, but I'll give a stab. (If interested in pursuing a critique from C# experts, by all means ask a related question and get a code/design review.) Here goes..
A method to get data should be in separate file. In your real version, this would have all the SQL code methods in one file. When calling the primary api, your data structures are now completely filled. (In large development systems, then other developers can stub out the method replacing with hard-coded dummy data, as you did. With this design approach, the code does not get messy when stubbing.
All the algorithmic methods discussed in this question should be in a separate file. The input is the data structures that were filled by the method to get data. This algorithmic class produces results in data structures that are related to this question.
Then these algorithmic results are sent to a graphics builder (possibly a separate file), and its results are sent to the view rendering methods, a separate file.
Breaking this program into at least three separate files (get data, algorithmic analysis, graphics view) lends itself to a clean design allowing for each class to be tested independently of the other classes.
I'll try to find time to learn C# by February. This will be my first project! Thanks again.
There appears to be a problem either with the algorithm or the graphics rendering. Below is the initial code in Case 1 (with 28-Sept just a replica of 29-Sept).
In Case 1, 30-Sept does not look correct since there is supposed to be overlapping.
In Case 2 and 3, I just tweaked the first appointment, and got results that appear to have some problems.
In Case 1, 30-Sept does not look correct since there is supposed to be overlapping.
In Case 2 and 3, I just tweaked the first appointment, and got results that appear to have some problems.
// CASE 1:
cb = new CalendarBox(1, new DateTime(2010, 9, 29, 11, 00, 00), new DateTime(2010, 9, 29, 11, 30, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(2, new DateTime(2010, 9, 29, 11, 00, 00), new DateTime(2010, 9, 29, 12, 00, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(3, new DateTime(2010, 9, 29, 13, 00, 00), new DateTime(2010, 9, 29, 13, 30, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(4, new DateTime(2010, 9, 29, 14, 15, 00), new DateTime(2010, 9, 29, 14, 45, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(5, new DateTime(2010, 9, 29, 11, 00, 00), new DateTime(2010, 9, 29, 15, 30, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(6, new DateTime(2010, 9, 30, 9, 00, 00), new DateTime(2010, 9, 30, 9, 30, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(7, new DateTime(2010, 9, 30, 9, 00, 00), new DateTime(2010, 9, 30, 11, 30, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(8, new DateTime(2010, 9, 30, 11, 00, 00), new DateTime(2010, 9, 30, 11, 30, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(9, new DateTime(2010, 9, 30, 12, 00, 00), new DateTime(2010, 9, 30, 13, 30, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(10, new DateTime(2010, 9, 30, 13, 00, 00), new DateTime(2010, 9, 30, 13, 30, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(11, new DateTime(2010, 9, 28, 11, 00, 00), new DateTime(2010, 9, 29, 11, 30, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(12, new DateTime(2010, 9, 28, 11, 00, 00), new DateTime(2010, 9, 29, 12, 00, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(13, new DateTime(2010, 9, 28, 13, 00, 00), new DateTime(2010, 9, 29, 13, 30, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(14, new DateTime(2010, 9, 28, 14, 15, 00), new DateTime(2010, 9, 29, 14, 45, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(15, new DateTime(2010, 9, 28, 11, 00, 00), new DateTime(2010, 9, 29, 15, 30, 00)); AllAppointments.Add(cb);
// CASE 2: One modification to first record:
cb = new CalendarBox(1, new DateTime(2010, 9, 29, 10, 00, 00), new DateTime(2010, 9, 29, 10, 30, 00)); AllAppointments.Add(cb);
// CASE 3: One modification to first record:
cb = new CalendarBox(1, new DateTime(2010, 9, 29, 10, 00, 00), new DateTime(2010, 9, 29, 11, 00, 00)); AllAppointments.Add(cb);
ASKER
Hi Phoffric
You have appointments spanning mulitple days...
This is currently not supported :)
Probably a typo I am assuming...
Line 12 for exapmle: cb = new CalendarBox(11, new DateTime(2010, 9, 28, 11, 00, 00), new DateTime(2010, 9, 29, 11, 30, 00)); AllAppointments.Add(cb);
You have appointments spanning mulitple days...
This is currently not supported :)
Probably a typo I am assuming...
Line 12 for exapmle: cb = new CalendarBox(11, new DateTime(2010, 9, 28, 11, 00, 00), new DateTime(2010, 9, 29, 11, 30, 00)); AllAppointments.Add(cb);
Hi dparnis,
Yes, it was a cut N paste typo; but despite the typo, 28-Sept came out OK; so I guess you are reasonably ignoring the date in the end time (since spanning days is not supported).
I fixed the end time to be 28-Sept. FYI Case 3 is the result from the below code. Just doing a little testing for you. Just wondering if this is the figure you expected for the below data.
Yes, it was a cut N paste typo; but despite the typo, 28-Sept came out OK; so I guess you are reasonably ignoring the date in the end time (since spanning days is not supported).
I fixed the end time to be 28-Sept. FYI Case 3 is the result from the below code. Just doing a little testing for you. Just wondering if this is the figure you expected for the below data.
cb = new CalendarBox(1, new DateTime(2010, 9, 29, 10, 00, 00), new DateTime(2010, 9, 29, 11, 00, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(2, new DateTime(2010, 9, 29, 11, 00, 00), new DateTime(2010, 9, 29, 12, 00, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(3, new DateTime(2010, 9, 29, 13, 00, 00), new DateTime(2010, 9, 29, 13, 30, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(4, new DateTime(2010, 9, 29, 14, 15, 00), new DateTime(2010, 9, 29, 14, 45, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(5, new DateTime(2010, 9, 29, 11, 00, 00), new DateTime(2010, 9, 29, 15, 30, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(6, new DateTime(2010, 9, 30, 9, 00, 00), new DateTime(2010, 9, 30, 9, 30, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(7, new DateTime(2010, 9, 30, 9, 00, 00), new DateTime(2010, 9, 30, 11, 30, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(8, new DateTime(2010, 9, 30, 11, 00, 00), new DateTime(2010, 9, 30, 11, 30, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(9, new DateTime(2010, 9, 30, 12, 00, 00), new DateTime(2010, 9, 30, 13, 30, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(10, new DateTime(2010, 9, 30, 13, 00, 00), new DateTime(2010, 9, 30, 13, 30, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(11, new DateTime(2010, 9, 28, 11, 00, 00), new DateTime(2010, 9, 28, 11, 30, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(12, new DateTime(2010, 9, 28, 11, 00, 00), new DateTime(2010, 9, 28, 12, 00, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(13, new DateTime(2010, 9, 28, 13, 00, 00), new DateTime(2010, 9, 28, 13, 30, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(14, new DateTime(2010, 9, 28, 14, 15, 00), new DateTime(2010, 9, 28, 14, 45, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(15, new DateTime(2010, 9, 28, 11, 00, 00), new DateTime(2010, 9, 28, 15, 30, 00)); AllAppointments.Add(cb);ASKER
hi phoffric
sorry, i just assumed that was the cause of the error...
I'm punching up the data now, and i'll see what i come up with.
sorry, i just assumed that was the cause of the error...
I'm punching up the data now, and i'll see what i come up with.
ASKER
Error with the conversion from SQL to Non-SQL
Forgot to sort by Start Date Time as well...
There should be two sorting calls instead of the one currently in the code...
I have pasted both of them below.
Let me know how you go...
// sort list
filteredBoxes.Sort(delegat
filteredBoxes.Sort(delegat
Forgot to sort by Start Date Time as well...
There should be two sorting calls instead of the one currently in the code...
I have pasted both of them below.
Let me know how you go...
// sort list
filteredBoxes.Sort(delegat
filteredBoxes.Sort(delegat
ASKER
i think also the ordering of the first sort call in the original code you would have downloaded is incorrect..
So delete the original filteredBoxes.Sort line and replace it with the two from the previous post.
So delete the original filteredBoxes.Sort line and replace it with the two from the previous post.
ASKER
I've also updated the zip file on the web server...
thanks for pointing out the issue...
let me know if you come across anything else...
thanks for pointing out the issue...
let me know if you come across anything else...
Nothing to be sorry about that :)
I got the latest zip, and will review your comments and test it some more tomorrow.
I got the latest zip, and will review your comments and test it some more tomorrow.
Here's another test. 29-Sept has shortened bars.
cb = new CalendarBox(1, new DateTime(2010, 9, 29, 9, 00, 00), new DateTime(2010, 9, 29, 12, 30, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(2, new DateTime(2010, 9, 29, 11, 00, 00), new DateTime(2010, 9, 29, 12, 00, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(3, new DateTime(2010, 9, 29, 8, 00, 00), new DateTime(2010, 9, 29, 11, 15, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(4, new DateTime(2010, 9, 29, 13, 00, 00), new DateTime(2010, 9, 29, 13, 30, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(5, new DateTime(2010, 9, 29, 14, 15, 00), new DateTime(2010, 9, 29, 14, 45, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(60, new DateTime(2010, 9, 29, 11, 00, 00), new DateTime(2010, 9, 29, 15, 30, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(6, new DateTime(2010, 9, 30, 9, 00, 00), new DateTime(2010, 9, 30, 9, 30, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(7, new DateTime(2010, 9, 30, 9, 00, 00), new DateTime(2010, 9, 30, 11, 30, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(8, new DateTime(2010, 9, 30, 11, 00, 00), new DateTime(2010, 9, 30, 11, 30, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(9, new DateTime(2010, 9, 30, 12, 00, 00), new DateTime(2010, 9, 30, 13, 30, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(10, new DateTime(2010, 9, 30, 13, 00, 00), new DateTime(2010, 9, 30, 13, 30, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(11, new DateTime(2010, 9, 28, 11, 00, 00), new DateTime(2010, 9, 28, 11, 30, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(12, new DateTime(2010, 9, 28, 11, 00, 00), new DateTime(2010, 9, 28, 12, 00, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(13, new DateTime(2010, 9, 28, 13, 00, 00), new DateTime(2010, 9, 28, 13, 30, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(14, new DateTime(2010, 9, 28, 14, 15, 00), new DateTime(2010, 9, 28, 14, 45, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(15, new DateTime(2010, 9, 28, 11, 00, 00), new DateTime(2010, 9, 28, 15, 30, 00)); AllAppointments.Add(cb);ASKER
I'm getting same issue...
As far as I can tell it seems to be a downside of the method outlined in ID: 33688649, unless I am missing something.
Maybe if we try to get max width by looping through each appointment and checking the adjacent rows until max row to see if it has a row of blanks next to it to allow it to fill out. Maybe this can be added in addition to the current stuff already being done for filling?
As far as I can tell it seems to be a downside of the method outlined in ID: 33688649, unless I am missing something.
Maybe if we try to get max width by looping through each appointment and checking the adjacent rows until max row to see if it has a row of blanks next to it to allow it to fill out. Maybe this can be added in addition to the current stuff already being done for filling?
Hmm, maybe this Case 4 diagram is acceptable. It's a matter of aesthetics and readability. For example, if the single task in the 2nd section ended at 8 pm, then the two short tasks in the 1st section certainly should have a width of 1.
Now, if we said that the two short tasks in the first section should have a width of 2, then there is a dilemma. Suppose that the single task in the 2nd section ended at time one of the short tasks begun. Then, going with a width of 2 for the short task, there would be a confusing diagram (at least in gray scale), since it would look like the long task in section 2 was actually a little longer.
Of course, if you can guarantee contrasting colors that when making black and white copies offers sharp delineation between the blocks, then extending the two short tasks can be considered.
So, it's a question of what your requirements are.
BTW - In the Oct-1 code below, if you modify the first entry's end time from 1500 to 1530, its position shifts from section 1 to section 2. Just wondering why that is.
Now, if we said that the two short tasks in the first section should have a width of 2, then there is a dilemma. Suppose that the single task in the 2nd section ended at time one of the short tasks begun. Then, going with a width of 2 for the short task, there would be a confusing diagram (at least in gray scale), since it would look like the long task in section 2 was actually a little longer.
Of course, if you can guarantee contrasting colors that when making black and white copies offers sharp delineation between the blocks, then extending the two short tasks can be considered.
So, it's a question of what your requirements are.
BTW - In the Oct-1 code below, if you modify the first entry's end time from 1500 to 1530, its position shifts from section 1 to section 2. Just wondering why that is.
cb = new CalendarBox(22, new DateTime(2010, 10, 01, 9, 00, 00), new DateTime(2010, 10, 01, 15, 00, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(21, new DateTime(2010, 10, 01, 9, 00, 00), new DateTime(2010, 10, 01, 10, 00, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(23, new DateTime(2010, 10, 01, 10, 30, 00), new DateTime(2010, 10, 01, 15, 00, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(24, new DateTime(2010, 10, 01, 11, 00, 00), new DateTime(2010, 10, 01, 17, 00, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(25, new DateTime(2010, 10, 01, 12, 30, 00), new DateTime(2010, 10, 01, 13, 30, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(26, new DateTime(2010, 10, 01, 14, 00, 00), new DateTime(2010, 10, 01, 15, 30, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(27, new DateTime(2010, 10, 01, 16, 00, 00), new DateTime(2010, 10, 01, 16, 30, 00)); AllAppointments.Add(cb);
cb = new CalendarBox(28, new DateTime(2010, 10, 01, 12, 30, 00), new DateTime(2010, 10, 01, 15, 00, 00)); AllAppointments.Add(cb);
It also looks like the yellow appointment time was squished a little more while the red appointment time is squished slightly more than the other two appointment times.
Still thinking on this. Without your code, it is like reverse engineering;) Maybe this isn't helpful but I thought pointing out what I see might help some.