What is the computational complexity of this method?

You'll need to post the algorithm for us to help tell you what it's computational complexity is.

Doug

As an example of complexity, lets consider SORTING.
Brute force sorting of N numbers compares each one with all the others, which is N x N, or quadratic.
Divide and conquer sorting is N log N, which is less expensive than N x N.
The ideal sorting algorithm does N iterations, wich is linear and the least expensive one.

What the revisor says is that your algorithm can be better, say, can be solved with less effort. It is not clear if the comment was on CPU time (probably yes) or Memory room.

Jose

So you need to calculate the support for every x,y pair. What function are you using for support? All pairs puts you at n^2 already.
If you have n nodes then there are n(n-1)/2 unique pairs so that in itself is O(n^2).

Thanks for the reply.

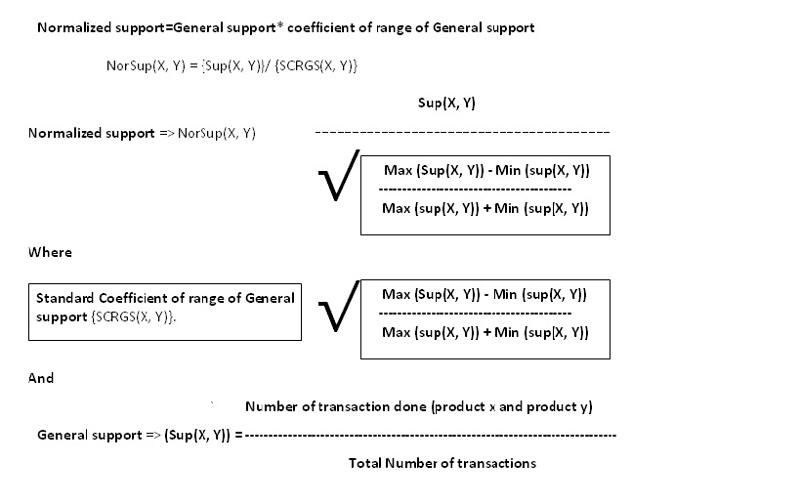
As you see I have no programs here . The formulat above calculates the Normalized Support.


Normalized support is used to define the minimum threshold value for the product combination based on the general support of the last two campaigns in order to maximize product sale. This should enable the marketing or the sales team to design future discount coupons or offers for product promotions. It can be said that Normalized support takes the general support to the next level.


Normalized Support Defined
see the formula above.

Methodology
Data Source
The paper makes use of data from a real grocery store to demonstrate the real world applicability of Normalized Support. The data was obtained from an anonymous store.

Real Data

A set of real grocery store data was used to demonstrate the scale of normalized support. It was part of a sales database of a grocery store chain. Point of sale data from four different stores in the area were collected in a central system with each transaction including the store code. The point of sale data were collected in a flat file and each record included the item discount coupons code (offer code), the store number and the Transaction identifier.

The first step of the analysis process involved data cleaning since some of the sales records lacked the Transaction identifier while the others lacked the offer code. This was followed by taking out the top nine products. The cleaning process eliminated around 49% of the total records. The outcome was a reliable dataset suitable for analysis. In this study, discount coupons were considered for a product.
      
In the second step, the text formatted data of transaction records was loaded into a SAS database for querying. Customer basket analysis involves finding the number of occurrences of every item to all other items to find possible relationships between them.
      
In order to make a practical analysis and identify the potential important items the study made use of a two step approach to screen data records. . The structure of sales data table items is illustrated in Fig. 1.1. The figure shows the items that were important to the analysis. The database as shown in Table Figure 1.1 demonstrates Normalized Support.
Data attributes:

TRANSID= Transaction ID [First three digits represents store id next 6 digit present transaction code]
PRODUCTS=PRODUCT ID
OFFER CODE=DISCOUNTED COUPONS CODE








 

TommySzalapski:

What function are you using for support?
see above please.

Thanks

So supp(x,y) = (count_transactions(x)+count_transactions(y))/count_transactions(all)?

Then your complexity is just O(n^2) where n is the number of products. That doesn't seem so bad to me.

The complexity of the overall calculation looks to be O(n^2 * k) where n is the number of x,y values you are considering and k is the number of transaction records per x,y pair.

Doug

By the way, is that how your paper actually looks? No offense, but your equations look really bad. You know that you can use Word's equation editor to make fractions and square roots and such right?

Right. I was assuming the counts of transactions were known already. If they are not known and you actually loop through them counting them one at a time, then you would need to add that in there. If the counts are already computed though, there's no need.

This screenshot is of an equation created in Word. You can make them look quite nice.
 

TommySzalapski:

Thanks for the reply.
no that is not taken from the paper. The paper looks better.
So you are saying the complexity is O(n^2 * k) then how it does not seem to be so bad? Me I think if the complexity is O(n^2 * k) then it is bad. Can you please tell me why it is not so bad.


dpearson:
Thanks for the help.
What do you think about this complexity O(n^2 * k) please?
If it is bad how we can optimize this?

Thanks

Jean

thanks for the image can I get an editable version

dpearson:
Thanks for the help.
What do you think about this complexity O(n^2 * k) please?
If it is bad how we can optimize this?

Good and bad are relative terms :)

I'd agree this looks fairly slow for large n and k.

To speed it up you should first compute sum(transaction(x)) for each x and store that as a cached value.  That step would be O(n * k), but requires space(O(n)) to store the totals.

Then the support calc would be a further O(n^2) - because now you can look up the sum(transaction(x)) in O(1).

So the total becomes O(n*k) + O(n^2) with O(n) additional space.  If k is less than n, this is O(n^2) overall - but that depends on the data set (can't tell from the algorithm's definition).

Doug

I've attached the Word file I used to create the equation. If you use 2003, then it won't work. But you can use the equation editor yourself and make the exact same thing.

Please answer this question.
You say Sup(X,Y) is the count of transactions of X and Y divided by the total transactions.
Are these counts already known or do you recount every time? If they are already known, then as I  mentioned before, you are only at O(n^2).

The transaction data appears to be in the database as a list of transactions - so it would require work to compute the counts.

Doug

I should have said that I'm assuming the database is correctly indexed.  If not, computing sum(transactions(x)) actually involves scanning all rows of the database - making it O(n*k) per summation operation instead of O(k).

But that's not likely the case.  Databases are good at indexing...

Doug

To help your algorithm in computation complexity (and not in space complexity) which changes.

n products
k transactions
l transaction details lines (entry of one product in a transaction)
t = average number of different products in a transaction (constant)

we agree that sup(X,Y) = sup(Y,X) [same pair = same support]

Instead of taking the problem by taking pairs of items, you could take the algorithm from the transactions side.

Each transaction includes a defined number of products (t), if you make a two dimensional map, indexed by product ID X and product ID Y, with as a value the number of common occurrences between product X and product Y.

Your support computation algorithm could be:

You would have a k loop over your transactions, and on each iteration, for each product id X in this transaction, take all other product ids Y (where Y>X) in the transaction, and increment the value support[X][Y]

Going over all transactions, and on each transaction loop through products (ask SAS to give you the data sorted by transaction id then product id) has a complexity of O(k) k loops of p*(p-1)/2 = O(k*p^2), but p being a constant (and small, you rarely have a 200 basket products), it is reduced to O(k)

The space complexity of the support map would be in O(n^2), use some efficient data storage for inserting values into the map and you will have a computation complexity of:
- O(k) if you use something like a two level hash table (a hash table linking to another hash table giving the requested value) (data input in a well designed hash table is O(1))
- O(k*log(n)) if you use something like a two level self balancing tree

Computing the total transactions count can be made in the same k loop, as soon as you see a product ID X, you increase a binary tree entry in O(log(n)) or hash table entry in O(1).

Hash tables are cheaper in CPU, but bigger in space, and must be well designed, because self increasing tables take a really long time to grow up, while trees are more reliable if not fine tuned.

You would have, to build your dataset, a:
- with a hash table structure: O(k)
- with a binary tree: O(k*log(n))


Hope this helped,
Julien

kiwi's right that you could trade space for time like this - but usually O(n^2) space isn't feasible for a large n.

Doug

That's the all point, not knowing the inputs makes it difficult to design, we're stuck with happy guesses...

But even a 10K products catalog would lead to something like:
- (10K*10K/2) = 50M values at worst case (at least one pair of each product X with each product Y)
- with 50 bytes each record (structure + data + pointers) --> 2,5G memory space

That's affordable for a SAS like server.

If you are on a major ecommerce site and want to try a n^2 on the entire 10M products catalog, then you'll have quite a problem :)

Julien

Or else if you have a n problem, then make the storage a SAS table or a small database, you'll be slow in access (way slower than in memory, in the order of a few milliseconds a read/write, so you'll want to optimize them), but you can scale easily.

We do that on some statistics computation in my company, with a few million possible products and many million users, it works efficiently (for our needs).

Julien

That's the all point, not knowing the inputs makes it difficult to design, we're stuck with happy guesses...

Fair enough :)

But usually you're best to assume O(n) for space in most algorithms - since the data itself that you start from is usually O(n) too so making extra copies of the data may be reasonable, but O(n^2) in space isn't usually safe to assume.

At least that's my opinion :)

Doug

And I completely agree with you Doug.

Preparing data beforehand would help a lot, and one would probably not compute all the supports between all products, but simply have the support of one top selling product to other significant products, making it easier in both memory and cpu.

Cheers,
Julien

TommySzalapski:

>You say Sup(X,Y) is the count of transactions of X and Y divided by the total transactions.
>Are these counts already known or do you recount every time?
yes we count them every time.

_kiwi_:

I am lost. I do not understand your solution to speed up. I do not know why you are concerned with the  space complexity here.  Can someone summarize the computation complexity and the solution please.

The optimization is about only reading the number of purchased items mines once, and not going through all products for each product you want to compute, giving O(k) instead of O(k+n^2), thus having a linear complexity.

The Space complexity concern is that to work this approach has to keep up to date an array containing, for each product, the number of times it can ne found with all other products, giving a potential array of n^2 elements, and you trade your computational complexity for a space complexity.

Then the algorithm you will choose will gave to tale into account the number of products (n) and the number of purchase lines (k) to be efficient.

If n is small and k huge, the array won't cost much in memory, and the time gain will be huge (only one loop). (top sellers scenario)

If on the other hand n is huge, the space taken by the array can be so important that this maked no sense to store the whole thing. (long tail scenario)

Cheers,
Julien

To restate, the computational complexity is a measure of the number of computing operations made by your program, given the hypothesis of data volume your program will process (number of products, number of purchase lines, number of customers, ...). 

The space complexity is the general idea of the memory amount that your program will require.

So what is the computational complexity if the counts are not known in advance? we count them every time.

And what is the computationaal complexity after the optimization please?

The computational complexity depends on the way you will implement your algorithm, what you have published so far is only a general presentation of a formula, not a real implementation, so the complexity of your exact implementation is something I can't give. From what you say it would be something like O(k+n^2)

The "optimized" version has, as stated, a O(k) computational complexity and a worst case O(n^2) space complexity.

 if I change the algorithm to the attached one will the complexity changes?

 

Hello,

To me, since the complexity of the algorithm is mainly contained in the "Number of transactions done (product x and product y)" statement, restating your algorithm this way does not change much the complexity.

Julien

Jean,

I think you're fundamentally confusing a formula and an algorithm.  A formula shows what the results of a calculation will be.  An algorithm shows the method for computing that result.  Algorithms include steps like loops and variables (for storage) which formulae can usually ignore.  It's a bit like the difference between a theorem and a proof - algorithms have more steps, a formula is just a summary.

As kiwi said, the question here is really how you're going to calculate "Number of transactions done" for the different product x,y.  There are different ways to do this (we've described several of them earlier in this question) and each has different computational complexity - from O(n*k) + O(n^2) using O(n) space down to O(k) using O(n^2) space.

Exactly what the complexity is depends on the precise method for computing the Sup(X,Y) value - which isn't specified in your problem description.

Hope that helps clarify things,

Doug

Yes. Can you post the actual algortihm you used when running experiments? Then we can help you much more specifically.

This question has been classified as abandoned and is closed as part of the Cleanup Program. See the recommendation for more details.