Zenoture
asked on
inflection points on f(x) using f''(x) graph
It's a question from my Calculus text book (Single Variable Calculus: Early Transcendentals by James Stewart 6th Edition), and the question states:
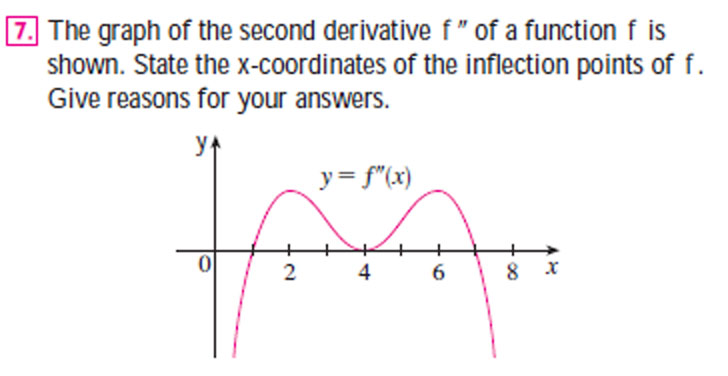
I understand why x = 1 and x = 7 are inflection points, because it is at those x's that the f''(x) returns 0 and changes direction or sign to positive or negative, causing the f'(x) function to have increasing or decreasing slopes @ those points.
What I don't understand is why x = 4 is NOT an inflection point? f''(4) = 0, and turns from decreasing to increasing... so what makes x=4 a special excluded case?

I understand why x = 1 and x = 7 are inflection points, because it is at those x's that the f''(x) returns 0 and changes direction or sign to positive or negative, causing the f'(x) function to have increasing or decreasing slopes @ those points.
What I don't understand is why x = 4 is NOT an inflection point? f''(4) = 0, and turns from decreasing to increasing... so what makes x=4 a special excluded case?
ASKER CERTIFIED SOLUTION
membership
This solution is only available to members.
To access this solution, you must be a member of Experts Exchange.
SOLUTION
membership
This solution is only available to members.
To access this solution, you must be a member of Experts Exchange.
If it goes slightly below 0 at x=4, then there would be two inflection points there, one when it crosses below 0 and another when it crosses back above.
what you have to do is think about curvature, if the second derivative changes sign then the curve changes between concave and convex
ASKER
So if I understood that right, the determining factor of inflection points ( and "decreasing" or "increasing" of f(x) ) is when f''(x) < 0 or f''(x) > 0?
SOLUTION
membership
This solution is only available to members.
To access this solution, you must be a member of Experts Exchange.
Yes, this is why the derivative can be understand as calculating the slope of a function
ASKER
Another issue I just noticed is, the image I posted (from the PDF version of the book) and the image I'm reading in the book are a bit different. In the book, there is a very tiny bump right below the x=4 mark, so wouldn't that technically mean that it did in fact cross and change signs for a brief moment to cross and change back?