mustish1
asked on
Prims and Kruskals algorithm
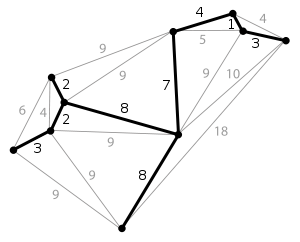
Hi guys: I give the name on each vertax a,b,c,d,e,f,g,h. Can any one please tell me how to find a minimal spanning tree and compute its total weight on this diagram?
Thanks.
qq2.jpg
Thanks.
qq2.jpg
ASKER
sorry
fh=5
cd=2
ce=8
fh=5
cd=2
ce=8
ASKER
ASKER CERTIFIED SOLUTION
membership
This solution is only available to members.
To access this solution, you must be a member of Experts Exchange.
ASKER
i want to do b ymyself. please let me know if i go wrong
ASKER
BC is the shortest arc with length 1.
so now BA and BE
BE is the shortest arc with length 2.
so now AC and AD
AD is the shortest arc with length 1.
AC create loop or circuit so we cant use it.
am i doing right?
so now BA and BE
BE is the shortest arc with length 2.
so now AC and AD
AD is the shortest arc with length 1.
AC create loop or circuit so we cant use it.
am i doing right?
SOLUTION
membership
This solution is only available to members.
To access this solution, you must be a member of Experts Exchange.
ASKER
so now DG and DF
DG is the shortest arc with length 8
DF is the shortest arc with length 7
EF is the shortest arc with length 3
FH is the shortest arc with length 5
GH is the shortest arc with length 6
I THINK REST OF THEM CREATE CIRCUIT
DG is the shortest arc with length 8
DF is the shortest arc with length 7
EF is the shortest arc with length 3
FH is the shortest arc with length 5
GH is the shortest arc with length 6
I THINK REST OF THEM CREATE CIRCUIT
ASKER
ONE MORE
DC is the shortest arc with length 2
DC is the shortest arc with length 2
ASKER
ASKER
Can experts please tell me if i did right
SOLUTION
membership
This solution is only available to members.
To access this solution, you must be a member of Experts Exchange.
SOLUTION
membership
This solution is only available to members.
To access this solution, you must be a member of Experts Exchange.
SOLUTION
membership
This solution is only available to members.
To access this solution, you must be a member of Experts Exchange.
ASKER
ASKER
is this is correct?
No you still have loops. I gave you the solution above in #37228420
Can you see why if you draw it?
Can you see why if you draw it?
SOLUTION
membership
This solution is only available to members.
To access this solution, you must be a member of Experts Exchange.
ASKER
> I gave you the solution above in #37228420
Why you start with 3 instead of 1 ?
Why you start with 3 instead of 1 ?
Actually you can start with any vertex. But, it is possible that when starting from different vertices, you will get multiple solutions all having the same minimum value.
Tom