Justin_Edmands
asked on
Drawing 3D coordinates in 2D screen space using python/pygame?
I am drawing 3D coordinates using Python/Pygame.
I KNOW this is meant to be accomplished using OpenGL/DirectX...
and I KNOW these calculations are meant to take place on a GPU...
but I don't care. I'm teaching myself the matrix transformations/projection
Since I've used XNA/C#, I'm trying to simulate the World*View*Projection Matrix math to calculate screen coordinates for 3D shapes.
Since I have worded the following issue very poorly, I attached my entire source file.
-I'm using numpy, with 4x4 homogenous matrices.
-My vertices all contain a fourth 'w' value of 1
If I have a simple shape, say a diamond, with 6 vertices:
(1, 0, 0), ( -1, 0, 0), (0, 1, 0), (0, -1, 0), (0, 0, 1), (0, 0, -1)
World Matrix is just an identity matrix.
vP = (0, 0.0, -2.0)
vR = (1.0, 0.0, 0.0)
vU = (0.0, 1.0, 0.0)
look = (0.0, 0.0, 0.0)
vL = look - vP
v1 = dotProduct(-vP, vR.T)
v2 = dotProduct(-vP, vU.T)
v3 = dotProduct(-vP, vL.T)
VIEW = np.matrix([
[vR[0,0], vU[0,0], vL[0,0], 0.0],
[vR[0,1], vU[0,1], vL[0,1], 0.0],
[vR[0,2], vU[0,2], vL[0,2], 0.0],
[v1, v2, v3, 1.0]
])
width, height = 640, 480
fov = math.pi / 2.0
aspect_ratio = float(width) / float(height)
z_far = 100.0
z_near = 0.1
PROJECTION = np.matrix([
[1 / tan(fov / 2) * aspect_ratio), 0, 0, 0],
[0, 1 / tan(fov / 2), 0, 0],
[0, 0, z_far / (z_far - z_near), 1],
[0, 0, (-z_near * z_far) / (z_far - z_near), 0]
])
(x, y, z, w) = world*view*projection*coor
and the final X, Y = x/w, y/w
Long story short, my "diamond" should appear well-formed... however this is what I see:
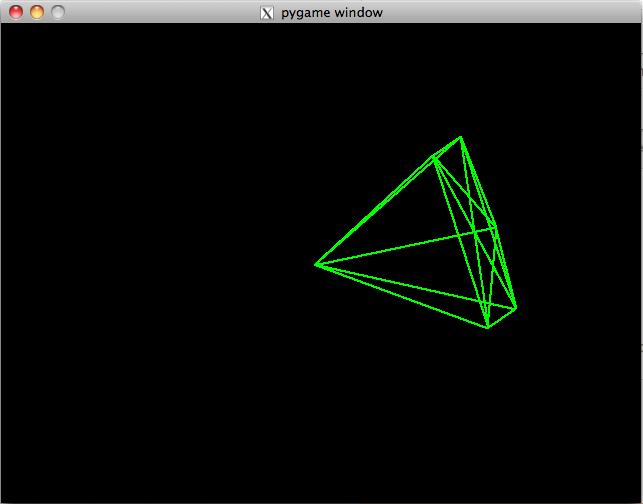 It SHOULD look like a symmetric diamond on all axes.
It SHOULD look like a symmetric diamond on all axes.
draw3d.py
I KNOW this is meant to be accomplished using OpenGL/DirectX...
and I KNOW these calculations are meant to take place on a GPU...
but I don't care. I'm teaching myself the matrix transformations/projection
Since I've used XNA/C#, I'm trying to simulate the World*View*Projection Matrix math to calculate screen coordinates for 3D shapes.
Since I have worded the following issue very poorly, I attached my entire source file.
-I'm using numpy, with 4x4 homogenous matrices.
-My vertices all contain a fourth 'w' value of 1
If I have a simple shape, say a diamond, with 6 vertices:
(1, 0, 0), ( -1, 0, 0), (0, 1, 0), (0, -1, 0), (0, 0, 1), (0, 0, -1)
World Matrix is just an identity matrix.
vP = (0, 0.0, -2.0)
vR = (1.0, 0.0, 0.0)
vU = (0.0, 1.0, 0.0)
look = (0.0, 0.0, 0.0)
vL = look - vP
v1 = dotProduct(-vP, vR.T)
v2 = dotProduct(-vP, vU.T)
v3 = dotProduct(-vP, vL.T)
VIEW = np.matrix([
[vR[0,0], vU[0,0], vL[0,0], 0.0],
[vR[0,1], vU[0,1], vL[0,1], 0.0],
[vR[0,2], vU[0,2], vL[0,2], 0.0],
[v1, v2, v3, 1.0]
])
width, height = 640, 480
fov = math.pi / 2.0
aspect_ratio = float(width) / float(height)
z_far = 100.0
z_near = 0.1
PROJECTION = np.matrix([
[1 / tan(fov / 2) * aspect_ratio), 0, 0, 0],
[0, 1 / tan(fov / 2), 0, 0],
[0, 0, z_far / (z_far - z_near), 1],
[0, 0, (-z_near * z_far) / (z_far - z_near), 0]
])
(x, y, z, w) = world*view*projection*coor
and the final X, Y = x/w, y/w
Long story short, my "diamond" should appear well-formed... however this is what I see:
 It SHOULD look like a symmetric diamond on all axes.
It SHOULD look like a symmetric diamond on all axes.draw3d.py
ASKER CERTIFIED SOLUTION
membership
This solution is only available to members.
To access this solution, you must be a member of Experts Exchange.
Glad to have helped, thanks for the points.
I've actually had to do this math myself for some jobs, including the clipping and rasterising sometimes. Not every platform has an OpenGL/Direct X type system. Sometimes you have to understand the math, so doing this is very useful.
I've actually had to do this math myself for some jobs, including the clipping and rasterising sometimes. Not every platform has an OpenGL/Direct X type system. Sometimes you have to understand the math, so doing this is very useful.
ASKER
In the end, I multiplied the transpose of each of those matrices in reverse... i.e. proj.T * view.T * world.T.
Thanks for the help! Now i'm gonna try drawing some complex shapes.