HansChr
asked on
Coordinate question for Matrix transformation in System.Drawing.Drawing2D
I have used a lot of time understanding the graphics class in C# because I need to make a program with function plotting.
I have gone through this interesting program about function plotting:
http://blog.csharphelper.com/2012/01/23/graph-an-equation-y--fx-in-c.aspx
I have understood the basic matrix transformation that makes objects rotate, flip, scale etc. but I still cant figure out one thing:
If you make a graphics transformation from world coordinates to page like this:
http://msdn.microsoft.com/en-us/library/749kbe3w.aspx
Then you get a coordinate system that is stretched vertically and horizontally to the sides of the picturebox:
But if you manually enter the values from the transformation matrix then you only get a small coordinate system that is centered correctly but isnt scaled properly:

How come the transformation matrix's scale values are not higher then? (look at the other attached screen capture.
If you print the matrix elements you get when x-min/max and y-min/max are -3,3, -3,3 by:
Matrix elements are then:
[m11,m12,m21,m22,dx,dy] = [5,96,0,0,-3,58,179,107,5]
If I instead enter the transformation Matrix by "hand" like this and of course make no other transformation before (remove the line: gr.Transform = new Matrix(rect, pts);):
I get the much smaller coordinate system if I draw the two lines:
In theory this is correct as far as I understand, because what actually happens is that the coordinate transformation is done by (look at the bottom of the page http://msdn.microsoft.com/en-us/library/w8s1ct0z) )
multiplying the original coordinates by the transformation matrix (here just for the x-axis):
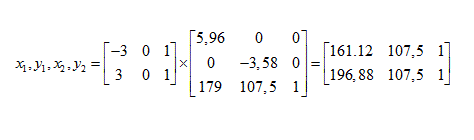
One can see that the pixel distance between the two coordinate sets are: 35,76. Then it is obvious why the coordinate system is so small.
My question is then: Why does the transformation matrix have scaling values that are so small and how does it stretch according to the first matrix constructor? This is very confusing. Its like the constructor adds something to stretch the rectangle to the border other than just the transformation matrix but I cant understand the theory and why.
If the scaling was greater in the transformation Matrix for example like this:
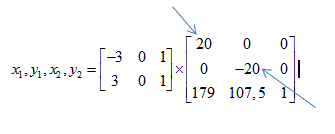
This would result in a larger coordinate system closer to the border of the picturebox:

I hope I have made myself clear and apologize if something is confusing.
Thanks a lot.
Regards
Hans
I have gone through this interesting program about function plotting:
http://blog.csharphelper.com/2012/01/23/graph-an-equation-y--fx-in-c.aspx
I have understood the basic matrix transformation that makes objects rotate, flip, scale etc. but I still cant figure out one thing:
If you make a graphics transformation from world coordinates to page like this:
int wid = picGraph.ClientSize.Width;
int hgt = picGraph.ClientSize.Height;
Bitmap bm = new Bitmap(wid, hgt);
Graphics gr = Graphics.FromImage(bm))
RectangleF rect = new RectangleF(xmin, ymin, xmax - xmin, ymax - ymin);
PointF[] pts =
{
new PointF(0, hgt),
new PointF(wid, hgt),
new PointF(0, 0),
};
gr.Transform = new Matrix(rect, pts);
gr.DrawLine(graph_pen, xmin, 0, xmax, 0);
gr.DrawLine(graph_pen, 0, ymin, 0, ymax);
{http://msdn.microsoft.com/en-us/library/749kbe3w.aspx
Then you get a coordinate system that is stretched vertically and horizontally to the sides of the picturebox:
But if you manually enter the values from the transformation matrix then you only get a small coordinate system that is centered correctly but isnt scaled properly:
How come the transformation matrix's scale values are not higher then? (look at the other attached screen capture.
If you print the matrix elements you get when x-min/max and y-min/max are -3,3, -3,3 by:
gr.Transform = new Matrix(rect, pts);
Matrix ele = gr.Transform;
float[] ele = inverse.Elements;
float el = ele.ElementAt(0);
float el2 = ele.ElementAt(1);
float el3 = ele.ElementAt(2);
float el4 = ele.ElementAt(3);
float el5 = ele.ElementAt(4);
float el6 = ele.ElementAt(5);
textBox1.Text += el.ToString() + " ";
textBox1.Text += el2.ToString() + " ";
textBox1.Text += el3.ToString() + " ";
textBox1.Text += el4.ToString() + " ";
textBox1.Text += el5.ToString() + " ";
textBox1.Text += el6.ToString();Matrix elements are then:
[m11,m12,m21,m22,dx,dy] = [5,96,0,0,-3,58,179,107,5]
If I instead enter the transformation Matrix by "hand" like this and of course make no other transformation before (remove the line: gr.Transform = new Matrix(rect, pts);):
gr.Transform = new Matrix((float)5.966666, 0, 0, (float)-3.583333, 179,107.5);I get the much smaller coordinate system if I draw the two lines:
gr.DrawLine(graph_pen, xmin, 0, xmax, 0);
gr.DrawLine(graph_pen, ymin, 0, ymax, 0);In theory this is correct as far as I understand, because what actually happens is that the coordinate transformation is done by (look at the bottom of the page http://msdn.microsoft.com/en-us/library/w8s1ct0z) )
multiplying the original coordinates by the transformation matrix (here just for the x-axis):
One can see that the pixel distance between the two coordinate sets are: 35,76. Then it is obvious why the coordinate system is so small.
My question is then: Why does the transformation matrix have scaling values that are so small and how does it stretch according to the first matrix constructor? This is very confusing. Its like the constructor adds something to stretch the rectangle to the border other than just the transformation matrix but I cant understand the theory and why.
If the scaling was greater in the transformation Matrix for example like this:
This would result in a larger coordinate system closer to the border of the picturebox:
I hope I have made myself clear and apologize if something is confusing.
Thanks a lot.
Regards
Hans
ASKER
.
ASKER
First of all thank you very much for your comment. I think we are very close to the solution.
I have to state that I pasted some of the code wrongly I appologize :
The code should have been and was indeed (I just accidently pasted the wrong code. So the problem is not because of this but thanks for noticing):
First of all if I copy your code in Visual Studio I get the following error:

I don't know why it won't cast. I read somewhere that if you only have old versions of net installed this method doesnt work but I have up to Net 4.0 installed.
Instead I tried this:
from: http://stackoverflow.com/questions/1970738/convert-system-array-to-string
This seems to work. But it doesnt change the output I get.
I also tried this:
from: http://stackoverflow.com/questions/3976707/what-is-the-fastest-way-of-converting-an-array-of-floats-to-string
This doesnt change the result either.
But I think I might have found the error:
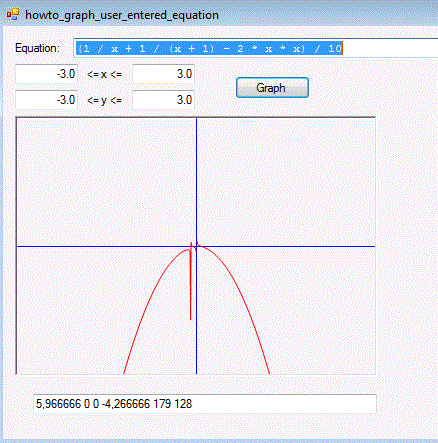
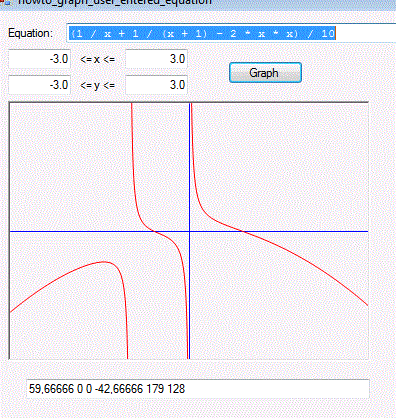
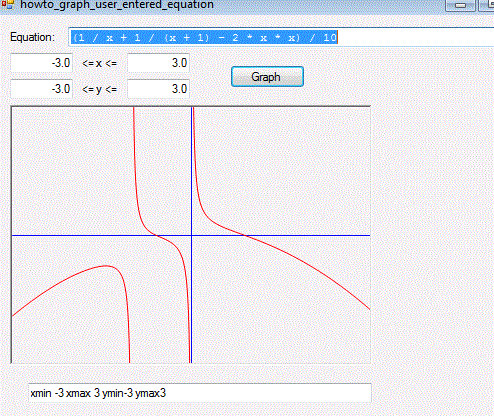
It seems like there are two different versions of the graph. One with user input enabled and one without. When I use the original input from the file downloaded here:
http://blog.csharphelper.com/2012/01/24/graph-an-equation-entered-by-the-user-in-c.aspx where user input is enabled I get this screenshot:
But if I use the other one at:
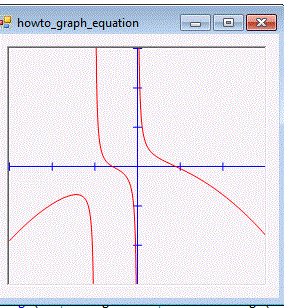
http://blog.csharphelper.com/2012/01/23/graph-an-equation-y--fx-in-c.aspx
I get this one:
I tracked the problem down to the difference in the code in the beginning of the program:
In the user input version the code for x-min/max and y-min/max come from user input:
In the other version code is:
Apparently the code gets translated wrongly somehow.
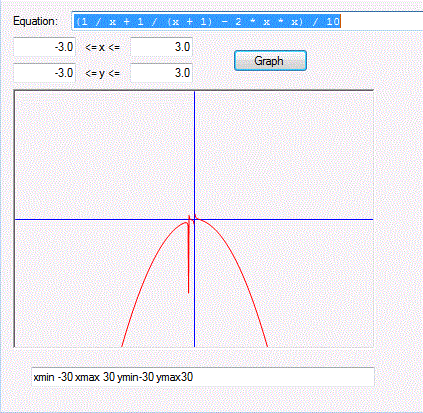
If I change the min and max values of the axis to -3,3,-3,3 I get the correct look and the correct coordinates:
The float values at input is apparently interpreted wrongly. Instead of x-min being float -3.0, 3.0 as inputted from the textbox its gets set to -30, 30 and the same for the y.axis.
Why I dont know.
I have to state that I pasted some of the code wrongly I appologize :
The code should have been and was indeed (I just accidently pasted the wrong code. So the problem is not because of this but thanks for noticing):
gr.Transform = new Matrix(rect, pts);
Matrix m = gr.Transform;
float[] ele = m.Elements;
float el = ele.ElementAt(0);
float el2 = ele.ElementAt(1);
float el3 = ele.ElementAt(2);
float el4 = ele.ElementAt(3);
float el5 = ele.ElementAt(4);
float el6 = ele.ElementAt(5);
textBox1.Text += el.ToString() + " ";
textBox1.Text += el2.ToString() + " ";
textBox1.Text += el3.ToString() + " ";
textBox1.Text += el4.ToString() + " ";
textBox1.Text += el5.ToString() + " ";
textBox1.Text += el6.ToString();First of all if I copy your code in Visual Studio I get the following error:
I don't know why it won't cast. I read somewhere that if you only have old versions of net installed this method doesnt work but I have up to Net 4.0 installed.
Instead I tried this:
string[] strings = Array.ConvertAll<float, string>(val, Convert.ToString);
textBox1.Text = string.Join(", ",strings);from: http://stackoverflow.com/questions/1970738/convert-system-array-to-string
This seems to work. But it doesnt change the output I get.
I also tried this:
string s = string.Join(" ", val.Select(f => f.ToString()).ToArray());
textBox1.Text = s;from: http://stackoverflow.com/questions/3976707/what-is-the-fastest-way-of-converting-an-array-of-floats-to-string
This doesnt change the result either.
But I think I might have found the error:
It seems like there are two different versions of the graph. One with user input enabled and one without. When I use the original input from the file downloaded here:
http://blog.csharphelper.com/2012/01/24/graph-an-equation-entered-by-the-user-in-c.aspx where user input is enabled I get this screenshot:
But if I use the other one at:
http://blog.csharphelper.com/2012/01/23/graph-an-equation-y--fx-in-c.aspx
I get this one:
I tracked the problem down to the difference in the code in the beginning of the program:
In the user input version the code for x-min/max and y-min/max come from user input:
float xmin = float.Parse(txtXmin.Text);
float xmax = float.Parse(txtXmax.Text);
float ymin = float.Parse(txtYmin.Text);
float ymax = float.Parse(txtYmax.Text);In the other version code is:
float xmin = -3;
float xmax = 3;
float ymin = -3;
float ymax = 3;Apparently the code gets translated wrongly somehow.
If I change the min and max values of the axis to -3,3,-3,3 I get the correct look and the correct coordinates:
The float values at input is apparently interpreted wrongly. Instead of x-min being float -3.0, 3.0 as inputted from the textbox its gets set to -30, 30 and the same for the y.axis.
Why I dont know.
ASKER
I think I found the error:
The author of the graph made a mistake in the property value of the textboxes containing the xmin/max ymin/max values:
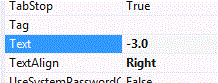
He made the decimal with a dot "." but it should have been a comma ",". If you put a dot it just get ignored and 3.0 will be interpreted as 30.
Of course I didnt notice that because it is the "start"-up proporty of the graph. If I change the proporty of all the 4 textboxes to "," instead of "." I get the correct answer.

Oh my God. I used 2 weeks thinking about this and the problem was a dot instead of a comma. I love computers :-/....
The author of the graph made a mistake in the property value of the textboxes containing the xmin/max ymin/max values:
He made the decimal with a dot "." but it should have been a comma ",". If you put a dot it just get ignored and 3.0 will be interpreted as 30.
Of course I didnt notice that because it is the "start"-up proporty of the graph. If I change the proporty of all the 4 textboxes to "," instead of "." I get the correct answer.
Oh my God. I used 2 weeks thinking about this and the problem was a dot instead of a comma. I love computers :-/....
ASKER CERTIFIED SOLUTION
membership
This solution is only available to members.
To access this solution, you must be a member of Experts Exchange.
ASKER
I see your point. Its the same with Excel with respect to decimals:
In regional settings I changed the "decimal symbol" from "," to "." and now the original code works :
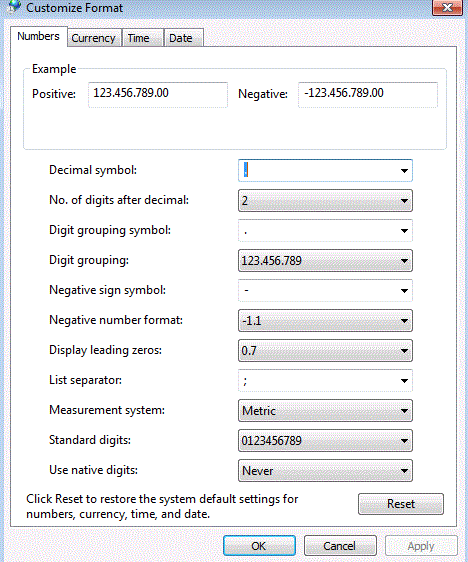
So it seems like a localized issue. Maybe changing to "British/american" doesnt change the "," to ".".
I didnt understand the last thing you wrote about being aware of the problem ;-).
Maybe the author could have made a case of "." and a case of "," to take the regional settings into account.
In regional settings I changed the "decimal symbol" from "," to "." and now the original code works :
So it seems like a localized issue. Maybe changing to "British/american" doesnt change the "," to ".".
I didnt understand the last thing you wrote about being aware of the problem ;-).
Maybe the author could have made a case of "." and a case of "," to take the regional settings into account.
> I didnt understand the last thing you wrote about being aware of the problem ;-).
Oh, think nothing of it, I just meant it seemed from your post that you had already come across the problem of printing 5,96 for m11 and in the code adjusting the comma to a decimal point.
> Maybe the author could have made a case of "." and a case of "," to take the regional settings into account
Well yes, that's the big question for me, if it should be handled by Visual Studio maybe.
Oh, think nothing of it, I just meant it seemed from your post that you had already come across the problem of printing 5,96 for m11 and in the code adjusting the comma to a decimal point.
> Maybe the author could have made a case of "." and a case of "," to take the regional settings into account
Well yes, that's the big question for me, if it should be handled by Visual Studio maybe.
ASKER
Well anyway thank you very much for your help ;-).
It seems like Visual Studio complains if I changed the decimal in regional settings from "," to "." and then changed the input to "3,0" but not the other way or something...
At least i wont make this mistake again!
It seems like Visual Studio complains if I changed the decimal in regional settings from "," to "." and then changed the input to "3,0" but not the other way or something...
At least i wont make this mistake again!
Open in new window
With the values this code returns (that differ from yours probably just because it's another Matrix) I can set it manually for the same size:Open in new window
Note that your code to print the elements uses 'ele' twice and actually prints the elements of the "Matrix inverse".