VB.Net DrawArc Inconsistent?
I'm using DrawArc to create arc segments. It's the usual "3 known points on a circle" routine.
When my graphics are oriented one direction, everything is fine (see below):
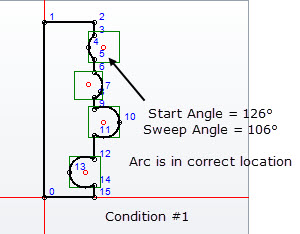
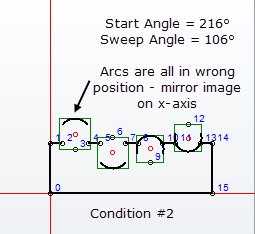
When I build the graphics with a different orientation, the segments are flipped around the x-axis (see below):
Note the values that are being sent to DrawArc(pen, rectangle, start, sweep). In Condition #1, the start angle is 126° and the sweep angle is 106°. The result is exactly what I would expect.
In Condition #2, the start angle is 216° and the sweep angle is 106°. The data is correct; the result appears like the start angle and resulting arc are a mirror image of what they should be. And this applies to all four arcs. It's almost like something is adding 180° to the start angle.
I'm using the same call to DrawArc for both conditions.
If my baseline for arcs is on a 45° angle, I also get erroneous results, but it appears like something is adding 90° to the start angle.
Thank you in advance for any suggestions!
George
When my graphics are oriented one direction, everything is fine (see below):

When I build the graphics with a different orientation, the segments are flipped around the x-axis (see below):

Note the values that are being sent to DrawArc(pen, rectangle, start, sweep). In Condition #1, the start angle is 126° and the sweep angle is 106°. The result is exactly what I would expect.
In Condition #2, the start angle is 216° and the sweep angle is 106°. The data is correct; the result appears like the start angle and resulting arc are a mirror image of what they should be. And this applies to all four arcs. It's almost like something is adding 180° to the start angle.
I'm using the same call to DrawArc for both conditions.
If my baseline for arcs is on a 45° angle, I also get erroneous results, but it appears like something is adding 90° to the start angle.
Thank you in advance for any suggestions!
George
ASKER CERTIFIED SOLUTION
membership
This solution is only available to members.
To access this solution, you must be a member of Experts Exchange.
ASKER
Excellent response - well documented and easy to follow.
Ok, great. Well don't hesitate to post further questions here if you're still stuck on this. Probably best to share a bit of code in that case of course.
ASKER
Thank you very much for your detailed response! I sincerely appreciate the effort you put into it and it was very easy to follow. Your sample is excellent!
I've still got an issue with Condition #2 - I can't get it to draw on the correct sweep. I haven't had much time to work on it for the past couple days, but I believe I have your code integrated into my project correctly. I suspect it may have something to do with the different coordinate systems in play.
As soon as I get the issue resolved, I'll update with the solution.
In the meantime, I will accept your answer as the solution and assume to problem is on my end.
Thank you!