chemicalx001
asked on
3d trilateration with multiple known points.
Hi all, I am attempting to write a C# trilateration function, but it is beyond my limited math knowledge...
I have a number of known points (currently 8, but this number may change)
I have the x, y, z coordinates for each.
P1[3];
P2[3];
P3[3];
P4[3];
P5[3];
P6[3];
P7[3];
P8[3];
P3[3];
where each array has 3 values, x, y and z.
I know the distance from the unknown point (x) to each of the known points.
double D1;
double D2;
double D3;
double D4;
double D5;
double D6;
double D7;
double D8;
So given these values, I need to find the xyz coordinates of the unknown point X[3];
What is the most straightforward way to do this? I have found examples in other code languages, but nothing that I understand in c#. And only ever with three points.
Any and all assistance would be much appreciated!
Thanks in advance!
I have a number of known points (currently 8, but this number may change)
I have the x, y, z coordinates for each.
P1[3];
P2[3];
P3[3];
P4[3];
P5[3];
P6[3];
P7[3];
P8[3];
P3[3];
where each array has 3 values, x, y and z.
I know the distance from the unknown point (x) to each of the known points.
double D1;
double D2;
double D3;
double D4;
double D5;
double D6;
double D7;
double D8;
So given these values, I need to find the xyz coordinates of the unknown point X[3];
What is the most straightforward way to do this? I have found examples in other code languages, but nothing that I understand in c#. And only ever with three points.
Any and all assistance would be much appreciated!
Thanks in advance!
There is no documentation of your used function anywhere.
Can you share at least its description (I am mostly concerned about point definition)
Also would be nice to share if geosphere is involved.
Can you share at least its description (I am mostly concerned about point definition)
Also would be nice to share if geosphere is involved.
trilateration is the intersection of 3 circles, triangles or spheres. So you need the x,y co-ordinates of the 3 points AND their radius
http://en.wikipedia.org/wiki/Trilateration#Preliminary_and_final_computations
http://en.wikipedia.org/wiki/Trilateration#Preliminary_and_final_computations
Makes little sense as 3 points look like dots to me in question...
ASKER
Hi Guys, thanks. these are the known points:
double x1 = P1[0];
double y1 = P1[1];
double z1 = P1[2];
double x2 = P2[0];
double y2 = P2[1];
double z2 = P2[2];
double x3 = P3[0];
double y3 = P3[1];
double z3 = P3[2];
and these are the distances from the unknown. (radius of circle)
double L1 = L[0];
double L2 = L[1];
double L3 = L[2];
I know i should get my head around the equation, but i am in a hurry to get this project finished! It seems to be working when i run it on 3 known points, the problem is, i have more than 3. I am trialling cycling through groups of 3 and averaging the result. Is this the best way to go about it?
Thanks again.
double x1 = P1[0];
double y1 = P1[1];
double z1 = P1[2];
double x2 = P2[0];
double y2 = P2[1];
double z2 = P2[2];
double x3 = P3[0];
double y3 = P3[1];
double z3 = P3[2];
and these are the distances from the unknown. (radius of circle)
double L1 = L[0];
double L2 = L[1];
double L3 = L[2];
I know i should get my head around the equation, but i am in a hurry to get this project finished! It seems to be working when i run it on 3 known points, the problem is, i have more than 3. I am trialling cycling through groups of 3 and averaging the result. Is this the best way to go about it?
Thanks again.
You must use integers to keep accuracy of numbers. Double will never yield any solution as around 1000 the detail is 1e-12
SOLUTION
membership
This solution is only available to members.
To access this solution, you must be a member of Experts Exchange.
ASKER
thanks! My issue is that am getting different results depending on which 3 points I use. Not ideal. So I am averaging the results. Which is working, but very slowly! Way too much latency to be of any use really.
So really my problem is with the trilateration not giving reliable results.
So back to my original question....
Does anyone have a C# formula to trilaterate the location of an unknown point from three known points (xyz) and distance from each known point to the unknown point?
Meanwhile, I will look into centroid, thanks.
So really my problem is with the trilateration not giving reliable results.
So back to my original question....
Does anyone have a C# formula to trilaterate the location of an unknown point from three known points (xyz) and distance from each known point to the unknown point?
Meanwhile, I will look into centroid, thanks.
ASKER CERTIFIED SOLUTION
membership
This solution is only available to members.
To access this solution, you must be a member of Experts Exchange.
ASKER
Thanks guys! I am reading up on RMS and getting better results. I also had an error in my code that was causing the lag, I was not clearing the list after i averaged it.
Thanks again for your help.
Thanks again for your help.
Thanks for the points. And one final note:
You more you know about the source or your errors, the better you can handle it.
In particular, the error function I showed earlier would be appropriate for errors in measuring the distance.
If the distance measurements were perfect, and the errors are in the coordinates of the base stations, you would not want to normalize with distance.
RMS Error = sqrt[ (Da - Dax)² + (Db - Dbx)² + (Dc - Dcx)² + . . . + (Dn - Dnx)² ]
You more you know about the source or your errors, the better you can handle it.
In particular, the error function I showed earlier would be appropriate for errors in measuring the distance.
If the distance measurements were perfect, and the errors are in the coordinates of the base stations, you would not want to normalize with distance.
RMS Error = sqrt[ (Da - Dax)² + (Db - Dbx)² + (Dc - Dcx)² + . . . + (Dn - Dnx)² ]
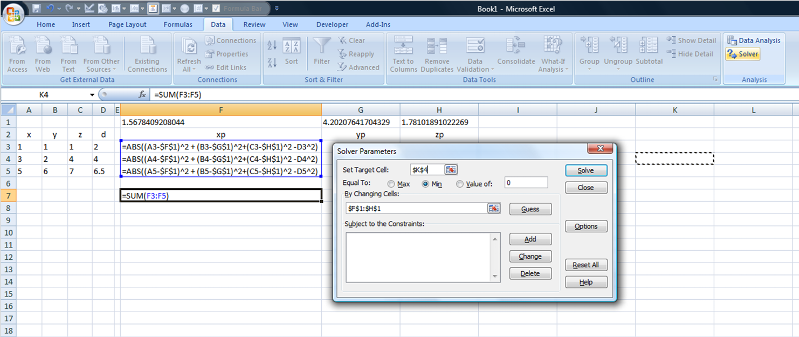
ASKER
I have trilateration working with three known points. I converted this example:
(https://www.experts-exchange.com/questions/21253179/triangulation.html)
to C#, and it seems to be going according to plan.
Now, to add more known points, would it be better to cycle through groups of three and merge the results somehow?
(groups of 4 would suit much better, but I am unsure how to add that function)
Or update the math to cope with eight points?
code as follows:
(note, converted but not really understood)
Open in new window
called:
Open in new window