Math between Excel and approximations
I need to find 2 values X1 and X2 which must respect next inequations and constrains:
Inequations:
1) (X1+X2)/360>=2.8E-03 or better >=3.0E-03 , ideal would be 3.2E-03 or 3.5E-03
2) 440*X1/(X1+X2)<350
3) 440*X2/(X1+X2)<200
4) 440*440*X1/[(X1+X2)*(X1+X2
5) 440*440*X2/[(X1+X2)*(X1+X2
Ideal would be to get at the 1) inequation the value >= as high as possible on the right side and at 4) and 5) inequations to get the values as low as possible at the right side as for example: at 4) instead of <1 to be <=0.6 and at 5) instead of <0.6 to be <=0.4.
Important to find the best matching values, no matter what method of calculations or approximation is used.
Any suggestions?
Inequations:
1) (X1+X2)/360>=2.8E-03 or better >=3.0E-03 , ideal would be 3.2E-03 or 3.5E-03
2) 440*X1/(X1+X2)<350
3) 440*X2/(X1+X2)<200
4) 440*440*X1/[(X1+X2)*(X1+X2
5) 440*440*X2/[(X1+X2)*(X1+X2
Ideal would be to get at the 1) inequation the value >= as high as possible on the right side and at 4) and 5) inequations to get the values as low as possible at the right side as for example: at 4) instead of <1 to be <=0.6 and at 5) instead of <0.6 to be <=0.4.
Important to find the best matching values, no matter what method of calculations or approximation is used.
Any suggestions?
ASKER
1) X1 and X2 ranges.
X1 may be between 50000 and 150000
X2 may be between 15000 and 50000
Generally speaking we may consider X1 and X2 between 15000 up to 150000, but will be restricted to lower values due to inequality constrains imposed.
2) The best matching values for X1 and X2 I do not know, but I referred to best matching value for X1 and X2 considering that will respect the inequalities 1), 4) and 5) in this way:
a. At 1) instead of >=2.8E-03 to be higher, ideal >=3.5E-03, but I can also survive with >=3.0E-03
b. At 4) instead of <1 to be <0.6, but I ca survive also with <0.7 or <0.8, because the <1 is the worst case.
c. At 5) is similar as at 4) only that instead of <0.6 to get <0.4
In such way can be understood X1 and X2 best matching values.
3) Do all "inequations" need to be "best matching", or a majority, or just one?
Basically 1) and 4) and 5), but would be better of course for all, meaning that at 2) and 3) to have lower numbers on the right side as for example at 2) instead of <350 to have <320 and at 3) instead of <200 to have <180.
You may use inequality instead of inequation if you like.
Inequation is still used as per Wikipedia:
https://en.wikipedia.org/wiki/Inequation
X1 may be between 50000 and 150000
X2 may be between 15000 and 50000
Generally speaking we may consider X1 and X2 between 15000 up to 150000, but will be restricted to lower values due to inequality constrains imposed.
2) The best matching values for X1 and X2 I do not know, but I referred to best matching value for X1 and X2 considering that will respect the inequalities 1), 4) and 5) in this way:
a. At 1) instead of >=2.8E-03 to be higher, ideal >=3.5E-03, but I can also survive with >=3.0E-03
b. At 4) instead of <1 to be <0.6, but I ca survive also with <0.7 or <0.8, because the <1 is the worst case.
c. At 5) is similar as at 4) only that instead of <0.6 to get <0.4
In such way can be understood X1 and X2 best matching values.
3) Do all "inequations" need to be "best matching", or a majority, or just one?
Basically 1) and 4) and 5), but would be better of course for all, meaning that at 2) and 3) to have lower numbers on the right side as for example at 2) instead of <350 to have <320 and at 3) instead of <200 to have <180.
You may use inequality instead of inequation if you like.
Inequation is still used as per Wikipedia:
https://en.wikipedia.org/wiki/Inequation
Thank you.
...and, again, for anybody wishing to contribute:
Are X1 &/or X2 whole numbers (i.e. not decimals) in the ranges you stated above?
If they can be decimal values, what level of precision (how many decimal places) are possible/practical?
...and, again, for anybody wishing to contribute:
Are X1 &/or X2 whole numbers (i.e. not decimals) in the ranges you stated above?
If they can be decimal values, what level of precision (how many decimal places) are possible/practical?
ASKER
X1 and X2 are natural numbers, without decimal value.
But if the constrains force the solution for decimal, then you may use 1 decimal point (0.0), because from practical reasons, due to tolerances, the decimal values will be ignored anyway. For the sake of calculations, ideal values, you may use 1 decimal point.
For example I found by trials in Excel, even if a graph I think will do better, solutions very close to the limits as X1=80000 and X2=45000. I am just wondering if I can get "better values", meaning to satisfy the inequalities from the right side for lower values to 4) and 5) and higher values at 1)
A graphic I found using next webpage:
http://goo.gl/xX1VXV
But if the constrains force the solution for decimal, then you may use 1 decimal point (0.0), because from practical reasons, due to tolerances, the decimal values will be ignored anyway. For the sake of calculations, ideal values, you may use 1 decimal point.
For example I found by trials in Excel, even if a graph I think will do better, solutions very close to the limits as X1=80000 and X2=45000. I am just wondering if I can get "better values", meaning to satisfy the inequalities from the right side for lower values to 4) and 5) and higher values at 1)
A graphic I found using next webpage:
http://goo.gl/xX1VXV
ASKER
Here is an additional note regrading the numbers X1 and X2.
X1 and X2 should match "preferred numbers" from electronics as described by IEC 60063 under E series.
X1 and X2 are in fact resistors values and the above inequalities are restrictions for current, voltage and power in a specific circuit.
https://en.wikipedia.org/wiki/Preferred_number
More exactly, X1 is a E48 type, meaning 2% tolerance and can have only next values, of course you can multiply with 10 or 100 or whatever, just add zeros at the end of the following numbers as you like:
E48 ( 2%): 100 121 147 178 215 261 316 383 464 562 681 825
105 127 154 187 226 274 332 402 487 590 715 866
110 133 162 196 237 287 348 422 511 619 750 909
115 140 169 205 249 301 365 442 536 649 787 953
And X2 is a E96 type, 1% tolerance and can have only next values, of course you can again just add zeros at the end of the following numbers as you like:
E96 ( 1%): 100 121 147 178 215 261 316 383 464 562 681 825
102 124 150 182 221 267 324 392 475 576 698 845
105 127 154 187 226 274 332 402 487 590 715 866
107 130 158 191 232 280 340 412 499 604 732 887
110 133 162 196 237 287 348 422 511 619 750 909
113 137 165 200 243 294 357 432 523 634 768 931
115 140 169 205 249 301 365 442 536 649 787 953
118 143 174 210 255 309 374 453 549 665 806 976
So far I found X1=78700 and X2=46400 matching the preferred numbers and respecting the above inequalities as best matching values.
Any other suggestion how to solve this and find a better pair solution?
X1 and X2 should match "preferred numbers" from electronics as described by IEC 60063 under E series.
X1 and X2 are in fact resistors values and the above inequalities are restrictions for current, voltage and power in a specific circuit.
https://en.wikipedia.org/wiki/Preferred_number
More exactly, X1 is a E48 type, meaning 2% tolerance and can have only next values, of course you can multiply with 10 or 100 or whatever, just add zeros at the end of the following numbers as you like:
E48 ( 2%): 100 121 147 178 215 261 316 383 464 562 681 825
105 127 154 187 226 274 332 402 487 590 715 866
110 133 162 196 237 287 348 422 511 619 750 909
115 140 169 205 249 301 365 442 536 649 787 953
And X2 is a E96 type, 1% tolerance and can have only next values, of course you can again just add zeros at the end of the following numbers as you like:
E96 ( 1%): 100 121 147 178 215 261 316 383 464 562 681 825
102 124 150 182 221 267 324 392 475 576 698 845
105 127 154 187 226 274 332 402 487 590 715 866
107 130 158 191 232 280 340 412 499 604 732 887
110 133 162 196 237 287 348 422 511 619 750 909
113 137 165 200 243 294 357 432 523 634 768 931
115 140 169 205 249 301 365 442 536 649 787 953
118 143 174 210 255 309 374 453 549 665 806 976
So far I found X1=78700 and X2=46400 matching the preferred numbers and respecting the above inequalities as best matching values.
Any other suggestion how to solve this and find a better pair solution?
ASKER
Oops, I made a mistake in the 1st inequality
Instead of “(X1+X2)/360>=2.8E-03 or better >=3.0E-03 , ideal would be 3.2E-03 or 3.5E-03”
It must be „360/(X1+X2)>=2.8E-03 or better >=3.0E-03 , ideal would be 3.2E-03 or 3.5E-03”
Under these circumstances the solutions are narrowed.
Here is the theory:
https://www.sophia.org/tutorials/graphing-systems-of-non-linear-inequalities
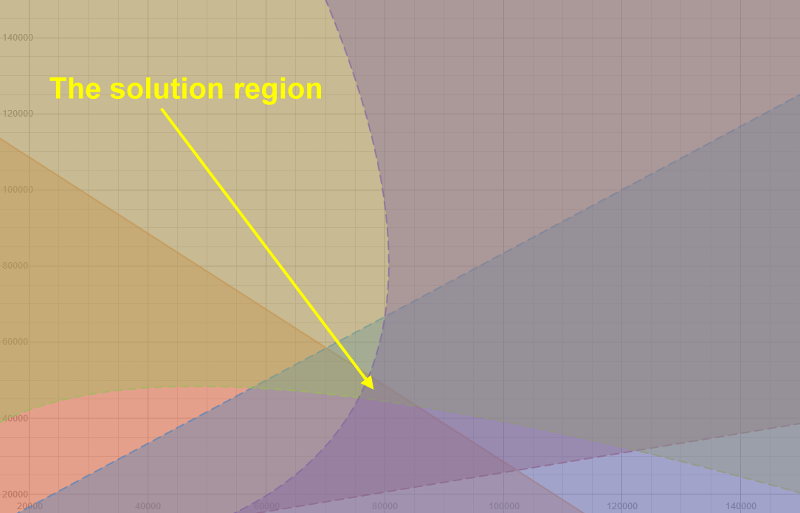
Using next online solver we see the region of the solutions:
https://www.desmos.com/calculator/tdtxtprhmn
Instead of “(X1+X2)/360>=2.8E-03 or better >=3.0E-03 , ideal would be 3.2E-03 or 3.5E-03”
It must be „360/(X1+X2)>=2.8E-03 or better >=3.0E-03 , ideal would be 3.2E-03 or 3.5E-03”
Under these circumstances the solutions are narrowed.
Here is the theory:
https://www.sophia.org/tutorials/graphing-systems-of-non-linear-inequalities
Using next online solver we see the region of the solutions:
https://www.desmos.com/calculator/tdtxtprhmn

Hi
you can use the solver add-in for excel to handle linear programming problems and get simplex optimised responses to problems, the add-in is available through the 'add-ins' manager and a brief tutorial is here:
http://www.msubillings.edu/asc/resources/math/Tutorials/FiniteMathHelps/Lin%20Prog%20with%20Excel.pdf
edit: just re-read your last post so my assumption that you meant 360/(x1... is correct. When I plug these into excels solver I do get a local optimised result but not a global one - Simplex generates an error indicating that one of the values may have gone negative - which clearly doesn't make sense for resistance (unless you inadvertently discovered a super conductor). but a non-linear solve gives a result in line with your quoted numbers from the earlier post with x1 appox 70000
I'm not any kind of expert in this field but I think you need further constraints in order to guarantee an optimum result from a mathematical perspective but in an engineering sense would it be correct to assume that a) any pair which generate a result in the solution set would be acceptable and b) certain resistor types will have an optimal set of values which may vary according to physical attributes and the optimal pairing would therefore depend on non mathematical factors?
you can use the solver add-in for excel to handle linear programming problems and get simplex optimised responses to problems, the add-in is available through the 'add-ins' manager and a brief tutorial is here:
http://www.msubillings.edu/asc/resources/math/Tutorials/FiniteMathHelps/Lin%20Prog%20with%20Excel.pdf
edit: just re-read your last post so my assumption that you meant 360/(x1... is correct. When I plug these into excels solver I do get a local optimised result but not a global one - Simplex generates an error indicating that one of the values may have gone negative - which clearly doesn't make sense for resistance (unless you inadvertently discovered a super conductor). but a non-linear solve gives a result in line with your quoted numbers from the earlier post with x1 appox 70000
I'm not any kind of expert in this field but I think you need further constraints in order to guarantee an optimum result from a mathematical perspective but in an engineering sense would it be correct to assume that a) any pair which generate a result in the solution set would be acceptable and b) certain resistor types will have an optimal set of values which may vary according to physical attributes and the optimal pairing would therefore depend on non mathematical factors?
ASKER
My previous found values X1=78700 and X2=46400 using trials in Excel cells with equations and just observations from my side are confirmed by the intersection/common region in the graph above.
How do you get negative numbers?
How do you get negative numbers?
I phrased that badly; I was using the Solver add-in which has various linear programming methods to automatically trial values and converge on an optimum solution. When using a linear method (the Simplex equation method) it hit an error condition and said one of the constraints had generated an invalid value - it doesn't tell you which one or why - since the only obvious error is a division by 0 it would indicate that it was either trying both values at 0 or one was the negative of the other. So its an artifact of the linear programming approach rather than an actual value.
Using an alternate method it converged on values of X1 from 69800 and above but warned that these were not a guaranteed global optimal because non linear methods cannot be extrapolated; however it would seem to confirm your own observations and I thought that if you had some time to investigate Solver and its various options it might help you explore the solution space.
- As I said I am not an expert , I'm just interpreting the Solver add-in output. when I've used solver in the past it was working with a quants analyst who handled the higher math whilst I did the problem setup
Using an alternate method it converged on values of X1 from 69800 and above but warned that these were not a guaranteed global optimal because non linear methods cannot be extrapolated; however it would seem to confirm your own observations and I thought that if you had some time to investigate Solver and its various options it might help you explore the solution space.
- As I said I am not an expert , I'm just interpreting the Solver add-in output. when I've used solver in the past it was working with a quants analyst who handled the higher math whilst I did the problem setup
ASKER
Thank you for explanations and Solver suggestion.
For the moment I will not try that, because the graphical approach narrows the results good enough in a small region where I can pick up the preferred number values.
Even more, if I change the restrictions values (=the number in the right side of the inequality) as:
- for inequality 1) 3.0E-03 or higher instead of 2.8E-3 then I can see that region disappears, becoming too small.
- for inequality 4) 0.9 or smaller instead of 1.0, then the same as above.
- for inequality 5) 0.5 or smaller instead of 0.6, then the same as above.
And I changed only one constrain at one moment of the time.
The above observations indicates that is not too much room to play and optimize the result and I should be happy with what I found, because they have to match also the real values of the resistors.
For the moment I will not try that, because the graphical approach narrows the results good enough in a small region where I can pick up the preferred number values.
Even more, if I change the restrictions values (=the number in the right side of the inequality) as:
- for inequality 1) 3.0E-03 or higher instead of 2.8E-3 then I can see that region disappears, becoming too small.
- for inequality 4) 0.9 or smaller instead of 1.0, then the same as above.
- for inequality 5) 0.5 or smaller instead of 0.6, then the same as above.
And I changed only one constrain at one moment of the time.
The above observations indicates that is not too much room to play and optimize the result and I should be happy with what I found, because they have to match also the real values of the resistors.
ASKER CERTIFIED SOLUTION
membership
This solution is only available to members.
To access this solution, you must be a member of Experts Exchange.
Hi viki2000, I'm glad you found the information you needed and hope the work goes well.
For future reference I'd note that you specifically asked for 'suggestions', which were given, and you will find people much more willing to respond on EE if you treat the time they devote to your requests with a little respect.
For future reference I'd note that you specifically asked for 'suggestions', which were given, and you will find people much more willing to respond on EE if you treat the time they devote to your requests with a little respect.
ASKER
@ regmigrant
I am really sorry that you felt disrespect from my side.
I relay have no problem to assign the points to someone who provides help, in this case your answers.
From my point of view, you can request the points to a supervisor and gladly I can give them to you.
I did not assign the points from beginning to you only because, even if you provided suggestions, they did not lead to solutions of my system inequalities and I did not even need to follow that path. I was just imagined that if 10 more people would have answered with suggestions, then I would have assigned the points to the person(s) who provided the (closest) solution(s) to my needs. That’s why I considered that I solved the problem by myself. It is not a question of disrespect.
Do you think I see it wrong?
If yes, then please ask the Zone Supervisor and you can have the 500 points for the Excel suggestion from my side, which I would have been probably considered valuable under other conditions.
I thank you for the suggestion and sorry if you felt bad, was no intention from my side.
I am really sorry that you felt disrespect from my side.
I relay have no problem to assign the points to someone who provides help, in this case your answers.
From my point of view, you can request the points to a supervisor and gladly I can give them to you.
I did not assign the points from beginning to you only because, even if you provided suggestions, they did not lead to solutions of my system inequalities and I did not even need to follow that path. I was just imagined that if 10 more people would have answered with suggestions, then I would have assigned the points to the person(s) who provided the (closest) solution(s) to my needs. That’s why I considered that I solved the problem by myself. It is not a question of disrespect.
Do you think I see it wrong?
If yes, then please ask the Zone Supervisor and you can have the 500 points for the Excel suggestion from my side, which I would have been probably considered valuable under other conditions.
I thank you for the suggestion and sorry if you felt bad, was no intention from my side.
I appreciate this wasn't done out of any malice and I'm not requesting points or feeling dis-respected; I meant the comment more for your own information as some experts will block you if you do this.
It is quite common for someone to solve their own problem without help from the experts, sometimes just having the discipline to phrase the question on here can help your thought process and allow a solution to become apparent. However once the question is posed the experts do spend time formulating responses and our only reward is the points; so even if you manage to figure it out on your own it's nice to either withdraw the question and say why, or split the points amongst those who responded as an acknowledgement that they took some time to help you.
Another point is that you were not asking for a 'solution', you asked only for suggestions so technically your question was answered even if it didn't resolve your 'problem' so its worth being specific about what you expect to award points for!.
Best of luck
Reg
It is quite common for someone to solve their own problem without help from the experts, sometimes just having the discipline to phrase the question on here can help your thought process and allow a solution to become apparent. However once the question is posed the experts do spend time formulating responses and our only reward is the points; so even if you manage to figure it out on your own it's nice to either withdraw the question and say why, or split the points amongst those who responded as an acknowledgement that they took some time to help you.
Another point is that you were not asking for a 'solution', you asked only for suggestions so technically your question was answered even if it didn't resolve your 'problem' so its worth being specific about what you expect to award points for!.
Best of luck
Reg
ASKER
Thank you for suggestion, but the solution was found with graphical approach after my research.
Sorry, not all of us use the terms "inequation" on a daily basis...
What is a "best matching value" (of either X1 or X2)?
Is that where the right side of the "inequations" are closest to the result of the corresponding left side without breaking the constraint imposed by the arithmetic comparison?
Do all "inequations" need to be "best matching", or a majority, or just one?