Math Question: What is the max distance of x?
What is the maximum distance of x in order to limit the slope change to less than .15 degrees?
SOLUTION
membership
This solution is only available to members.
To access this solution, you must be a member of Experts Exchange.
SOLUTION
membership
This solution is only available to members.
To access this solution, you must be a member of Experts Exchange.
ASKER CERTIFIED SOLUTION
membership
This solution is only available to members.
To access this solution, you must be a member of Experts Exchange.
SOLUTION
membership
This solution is only available to members.
To access this solution, you must be a member of Experts Exchange.
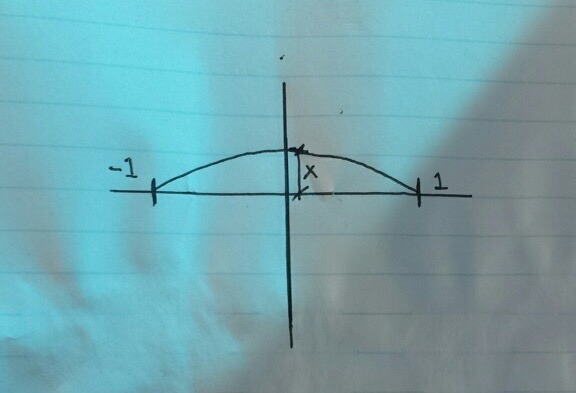
What is the curve? A circle or a parabola or something else?
Are you launching a rocket or a car?
Are you shooting a bullet or a canon ball? How fast is it going at the start?
And did you really mean 0.15 degrees? That is such a small angle that it is difficult to measure it by hand.
The slope is slightly positive to the left at -1. It is slightly negative to the right at +1.
A change of 0.15 degrees could mean that it starts at +0.075 degrees and changes to -0.075 degrees. Is this what you want?