Numerical reasoning - lowest price
How do I go about this?
5 liters but they come in 4 packages --> $11.95 - $2.49 to give me 4 packages out of 5 .. not sure if I'm on the right track
5 liters but they come in 4 packages --> $11.95 - $2.49 to give me 4 packages out of 5 .. not sure if I'm on the right track
ASKER CERTIFIED SOLUTION
membership
This solution is only available to members.
To access this solution, you must be a member of Experts Exchange.
SOLUTION
membership
This solution is only available to members.
To access this solution, you must be a member of Experts Exchange.
SOLUTION
membership
This solution is only available to members.
To access this solution, you must be a member of Experts Exchange.
SOLUTION
membership
This solution is only available to members.
To access this solution, you must be a member of Experts Exchange.
ASKER
$11.85 :)
Right. By eliminating the (3) and (1,1), you quickly get to (2,2,1) --> $11.85
In fact, you have also eliminated 5. So you have the solution for any integer.
ASKER
Going to get a numerical reasoning book after I get an offer. I'm close to an offer from a place I interviewed with today. Good to keep practicing.
To keep practicing, extend this problem to have, say, 10 kinds of packages and ask yourself how can you methodically eliminate packages as done in earlier posts. By generalizing a simpler problem to the same kind of problem, but with more items, you start seeing algorithmic patterns that become part of your toolbox.
Good luck in getting your better job!
Good luck in getting your better job!
ASKER
Good luck in getting your better job!
Thanks!
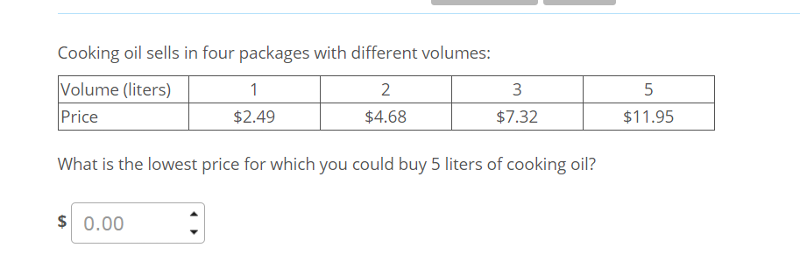
ASKER